简单来说,我们可以对A和B、A和C分别做简单线性相关,如果,两个相关系数均没有统计学意义(即p均>0.05),那也没有必要比较A和B还是和C更相关了。所以,咱们的前提是:A和B、A和C之间的相关系数有统计学意义(即p均<0.05)。
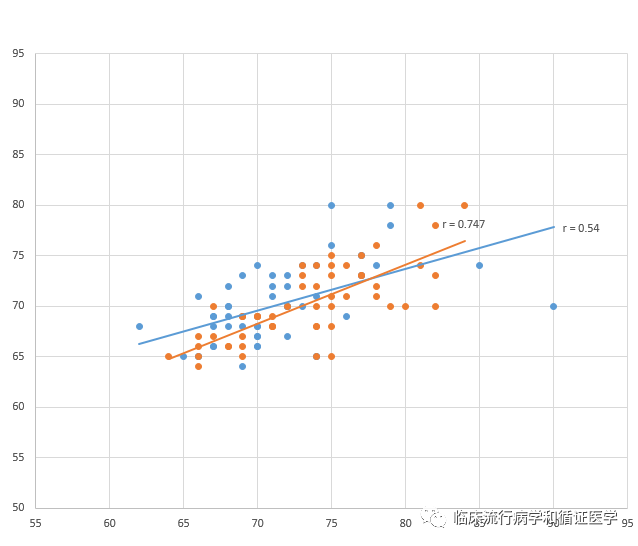
比如,图中蓝线代表的是A和B,橙线代表的是A和C。
SPSS给出的结果如下表,两个相关系数均有统计学意义,其中r_AB=0.54(p<0.001),r_AC=0.747(p<0.001)。表面看上去,r_AC>r_AB,是不是说明A和C之间更相关呢?
我们知道单纯比较并不可靠,如果有适当的统计学检验能加以佐证结果,就比较有说服力了。首先,我们可以分别求出两个相关系数的置信区间,然后考察两个区间的关系,以比较两个相关系数。
其实求相关系数的置信区间很简单,在简单相关的界面,选中自助抽样(英文为Bootstrap),选择执行自助抽样。
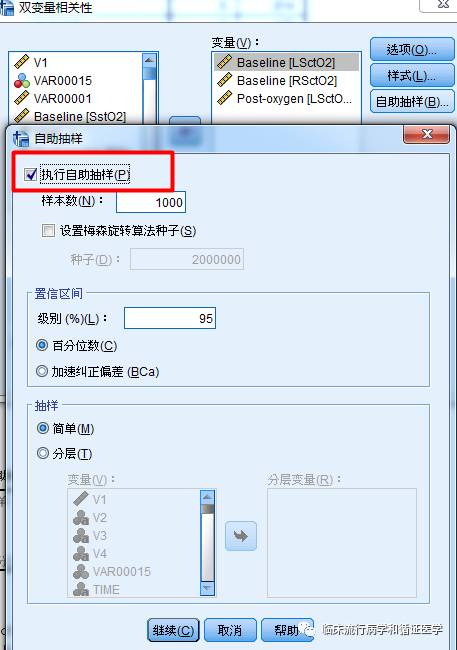
咱们看SPSS的结果,r_AB=0.54,区间为0.353至0.747;r_AC=0.747,区间为0.618~0.857。二者的置信区间有交叉,说明两个相关系数的差异是没有统计学意义的,也就是说,通过统计学检验,两个相关系数是一样的,并不是我们认为的A和C更相关。
当然,还有另外一种方法,只需要知道相关系数r和样本量n。刚刚的例子中,r_AB=0.54,r_AC=0.747,样本量均为54,可求出

u值服从标准正态分布,如果u>1.96或者u<-1.96,则说明p<0.05;如果-1.960.05。例子中u= -1.828,在 -1.96和1.96之间,说明p>0.05,两个相关系数在统计学上没有差异。当然,有读者会提出如果相关系数是负的怎么办呢,因为我们考察的是相关程度,直接用相关系数的绝对值即可。


