Fisher是英国统计与遗传学家,现代统计科学的奠基人之一,并对达尔文进化论作了进一步工作。安德斯·哈尔德称他是“一位几乎独自建立现代统计科学的天才”,几乎现在经典的统计方法都有他的贡献。Fisher精确检验便是以他的名字命名的统计方法,这个统计方法也和他本人一样牛,可以将所有R×C列表的精确概率计算出来。但在应用Fisher精确检验时常有比较严格的条件,为什么要设定这些条件呢?另外Fisher精确检验没有卡方值,它是怎么得到p值的呢,这需要从其计算过程说起。
Fisher精确检验的计算原理如下:
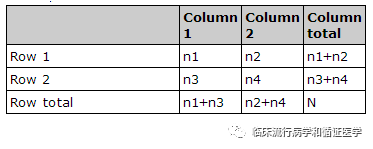
首先保持求和的数字(n1 n2,n3 n4,n1 n3,n2 n4)不变的情况下,变换n1、n2、n3、n4四个数字,会出现多种组合。如

上表变换会有以下4种组合
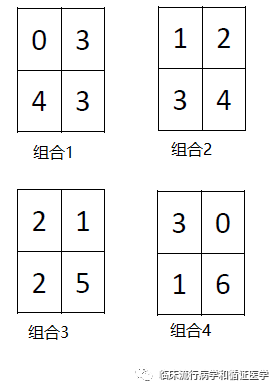
每种组合的概率可以求出来,公式如下:
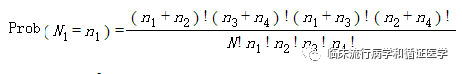
以上四种组合的概率分别为0.167,0.5,0.3,0.033,各组合概率和为1。我们需要的Fisher精确检验的p值(双侧)为小于等于当前组合(组合1)的概率之和。由于当前组合(组合1)的概率为0.167,Fisher精确检验的p=0.167 0.033=0.2.
由以上计算过程可见,Fisher精确检验直接将概率求和得到p,而不是根据卡方值和自由度查表得到的,因此Fisher精确检验不提供卡方值。其次上述计算过程的计算量非常大,当样本稍大时,组合数会成倍成长,同时每个组合的概率计算需要大量阶乘计算,这在计算机出现之前,进行大样本的Fisher精确检验是不可能的。因此在早期只有在小样本时才使用Fisher精确检验,这个条件就是样本量小于40或者某个格子的期望数小于1。
当然,话说回来,现在计算机的计算能力有了较大发展,是不是可以用Fisher精确检验代替pearson卡方检验呢?这个问题可能大家有不同的看法,一方面我个人并不支持这种替代,因本较大样本时,pearson卡方检验结果非常接近Fisher精确检验的结果,但pearson卡方检验计算非常简单,手工即可完成,使用较方便;另外一方面,个人觉得可适当放宽Fisher精确检验的条件,如果期望值在1-5之间或者高于40但不太大时,使用了Fisher精确检验也不用认为有错误。


