我们在进行多重线性回归分析时,往往需要选择自变量的筛选方法,如进入法、前进法、后退法和逐步法等。这些方法之间有什么区别呢?它们是如何工作的呢,本文就来跟大家聊聊这一问题。
计算机就是一台没有思想的算法工具,那么在某一个特定的问题面前,计算机是如何进行影响因素筛选的呢(也就是自变量的筛选)?这些都是算法程序员给它定的规则,计算机只需要执行这一规则即可。
在多重线性回归自变量的筛选上,终极规则是:1、模型中留下有用的自变量,剔除没用的自变量;2、模型要有较高的预测价值;3、模型要简约,即方程的自变量要尽可能的少。规则定了,那么通过哪一个数值来体现这个规则呢?
常用的统计量有以下几个:1、调整决定系数:调整决定系数跟决定系数不同,它会受到自变量个数的“惩罚”,调整决定系数越大,模型越好。2、Cp统计量:Cp统计量是基于残差平方和的一个原则,按Cp统计量应该选择除全模型外Cp值与(P 1)最接近的模型。3、AIC统计量:AIC是源于极大似然估计,按AIC准则应该选择使AIC最小的模型。
有了上述的判断统计量之后,我们就可以建立不同的模型了,然后挨个比较各个模型上述统计量的差别,最终选出最好的模型。那么不同的模型是怎么建立的呢?最简单的方法就是枚举法,也就是不停地尝试,直至遍历。这也是一个重要的自变量选择方法,专业上叫做全局择优法。
比如我们现在有4个自变量,应用全局择优法可以建立以下模型:
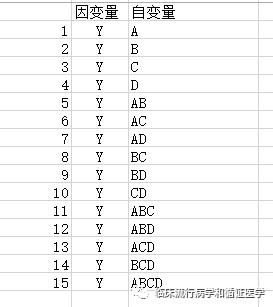
对上述15个模型分别计算其调整决定系数、Cp或AIC的大小,然后选择一个最合适的模型。这就是全局择优法,但它有一个缺点就是计算量很大,尤其是当自变量量个数较多时,如果有10个自变量,方程的个数为2的10次方-1=1023个。另外全局择优法是对自变量的组合进行的择优,所以不能保证组合里面一定没有滥竽充数的。
于是便有了“逐步选择法”,逐步选择法按照自变量选入的顺序不同,分为前进法、后退法和逐步回归法:
前进法:是方程中自变量从无到有、由少到多的过程。它的做法是首先将每个自变量与因变量做回归,挑出一个影响最大的,做假设检验后先进入方程。然后在余下的自变量中,考虑先前进入的自变量的情况下,再挑偏回归平方和大的自变量进入方程。依此类推,直到没有合适的自变量可以引入。
后退法:与前进法正好相反,是方程中的自变量由多到少,逐渐精简的过程。首先是把所有自变量都放进去,然后计算每个自变量的偏回归平方和,剔除偏回归平方和最小的一个(此过程也需要做统计推断)。然后再对剩余的自变量进行类似的筛选,直至无自变量可被剔除。
逐步法:该方法的本质是前进法,但是每引入一个新的自变量后,都需要对方程中旧的自变量做检验,判断其是否还有存在的价值。依此类推,直至方程稳定,不再有自变量进入或退出。
前进法的局限性是后续引入的自变量可能会使之前引入的自变量变得不重要,其优点是可以自动去掉高度相关的自变量;而逐步法正好遗传前进法的优点,又有效地避免了其缺点。后退法选中的自变量数目一般会比前进法多,其缺点时不能有效避免某些高度相关的自变量。
最后值得提醒的是;不要盲目信任回归分析所得到的结果,在这些判断准则下得到的所谓“最优”方程并不一定是最好的。理想的做法是,研究者还应该结合问题本身和自己的专业知识来共同判断。


