近日有读者提出能否介绍一下,非劣效试验的统计分析过程,本文将向读者简单介绍一下该部分内容。
非劣效试验的统计分析方法与常规的生物统计学类似,其原则是一样的,都是基本的医学统计分析过程。我们知道统计分析分为统计描述和统计推断,统计描述是对样本的统计量进行一些描述;统计推断是用样本量统计量来推断总体的参数,或者推断两个样本是否来源于同一个总体。
统计推断又分为参数估计和假设检验,参数估计就是用样本统计量去估计总体参数,可分为点估计和区间估计;假设检验在大部分情况下是检验不同样本是否来源于同一个总体。假设检验存在两个假设,一个是原假设(H0),一个是备择假设(H1),它是利用小概率的思想求证原假设发生的概率,再用反证法推断备择假设是否成立。
聊了这么对,跟非劣效有半毛钱关系?当然有关系,非劣效试验的统计推断也是分为两类:参数估计和假设检验,下面将分别叙述。举个例子,假设需要比较试验药物T和对照药物C的疗效E(t)和E(c)的差别,非劣效界值为Δ。
一、参数估计
参数估计就是求对照药物与试验药物的疗效差值的可信区间,看看这一可信区间是否包含非劣效界值,如果包含则得不出非劣效的结论。这儿涉及几个问题:1、疗效的评价是大好,还是小好?比如对高血压患者降压,那么血压在适当的范围内是降低的越多越好(此类指标称为低优指标);又比如对贫血患者升高血红蛋白,也是在适当的范围内升高的越多越好(此类指标称为高优指标)。2、可信区间的选择可以是双侧95%的一侧,也可以是单侧97.5%。3、非劣效界值的确定,这是一个难题,需要统计学人员和临床研究者共同讨论决定,之前本微信号也有文章讨论过这个问题,可以查阅。
参数估计的结果判断如下图(此图源自参考文献):
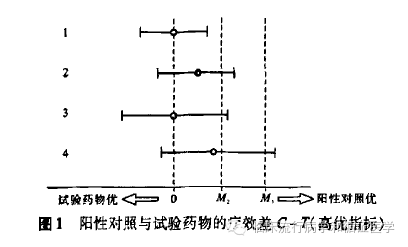
图中有3条竖线,第一条表示E(c)-E(t)=0(即C与T相等),第一条表示E(c)-E(t)=M2(M2为非劣效界值),第一条表示E(c)-E(t)=M1(M1为阳性对照药相对于安慰剂的疗效)。图中有4条带圈的横线,这是不同研究的C-T的点估计和区间估计值。
依据图来判断:第1条横线的显示为试验药非劣效于阳性药结果;第2和3条横线的显示不确定试验药为非劣效于阳性药,但可间接推断优于安慰剂;第4条横线显示试验药疗效不优于安慰剂组。注意此图为高优指标,低优指标依次类推。
2、假设检验
非劣效检验也可以采用假设检验进行比较,首先建立检验假设(以连续性变量高优指标为例),原假设为:C-T≥Δ,备择假设为:C-T<Δ,alpha=0.025。均数比较的计算公式为:
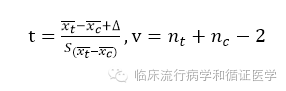
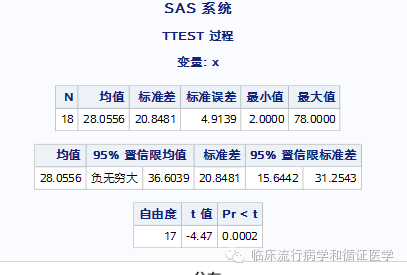
SAS示例程序为:
procttesth0=50alpha=0.05 sides=L;
var x;
run;
计算结果为: