近来很多过来咨询的医生在做完某指标的假设检验后,想用这个指标去做预测,例如病例组的血压(155±10mmHg)与对照组的血压(110±10mmHg)差异有统计学意义,就想用血压去预测是否发病,但往往预测结果并不理想;还有一个现象就是有的指标在进行假设检验时p值很小,但预测能力并不好,反而有些指标p值不太小,预测能力更高一些。今天以t检验为例,从统计分布的角度看一看为什么会出现这些现象。
首先我们看一下t检验的公式:
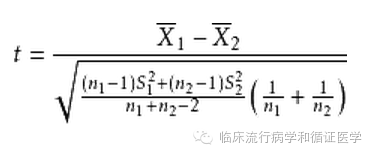
上公式中,X代表平均值,S代表标准差,n代表样本量。从公式可以看到,t检验的t值大小由两组的均值差、标准差和样本量决定,t值和样本量大小决定了p值大小,总体来说,p与均值差成反比,与标准差成正比,与样本量成反比。
预测模型的好坏由界值判断的准确率决定。为方便讨论,我们模拟正态分布、标准差相同的两组数据。下面分别用R产生对照组(均值=5,标准差=2)和病例组(均值=12,标准差=2)的正态分布数据各1000个,其直方图如下:
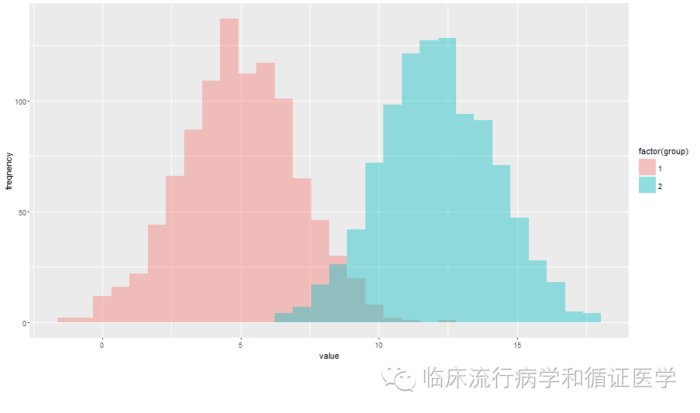
所谓做预测就是找一个界值,将产生的数据分为患病(高于界值)和无病(低于界值)然后与实际是否患病做比对,得到灵敏度、特异度等。上图中无轮如何选择界值,都不可能完全分开,但可以找到一个最优值使判断准确的比例最高,如选择8或者9可能较好。
预测指标好坏与图形中重叠部分有关,重叠越小,判断准确越高。重叠比例与谁有关呢?直接从图中可以看出与重叠部分大小与两组差值有关,差值变大,相当于两个直方图向两侧移动,两组分散较开,重叠就小。另外与标准差有关,均值不变,标准差都变为4,分布图如下,可见重叠变大。
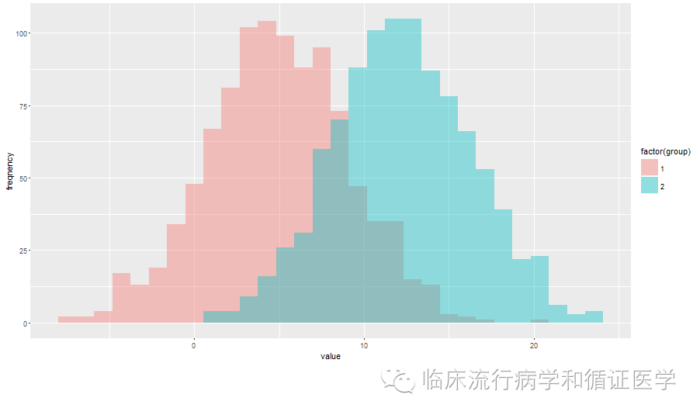
重叠区域与样本量有关吗?下面我们将均值、标准差不变,将样本量都变为2000,结果如下图。
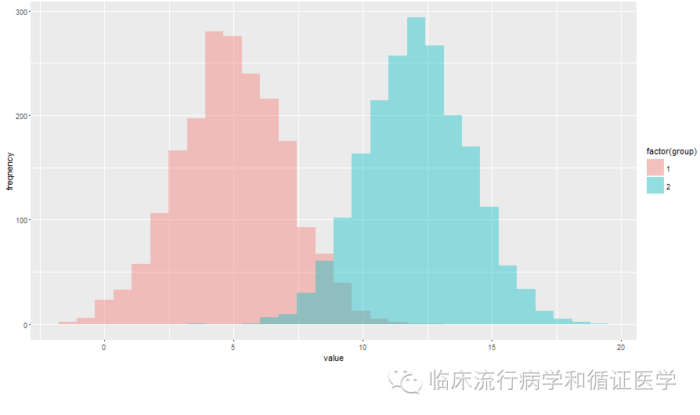
重叠区域基本没有变化。这个也比较好理解,样本量2000时相当于将两个样本量1000的数据合并一起,数据变密集了,但均值和分布宽度没有变化。从上可以看出,预测能力与两组均值差和标准差有关,与样本量无关。
对比上面的结论可以发现,t检验的p值由三个指标决定,而预测能力大小只与两个指标有关,也即是说,如果保持均值差和标准差不变,预测准确度基本不变。但扩大样本量,p值可变小,因此p值大小与预测能力无必然的关系,不能用p值大小判断该指标的预测价值,特别是在大样本的临床研究中,如果某指标差异有统计学意义,并不代表该指标有较好的预测价值。


