这样比较显然是不对的,因为它会增加犯Ⅰ类错误的机会。很多研究者知道在多组均数比较时,如果方差分析差异有统计学意义,那么我们还可以做post-hoc的检验,通常采用的方法是SNK、LSD、Bonferroni和Sidak法。其原理可以表达为,如果是三组间两两比较,需要比较3次,那么每次都不发生Ⅰ类错误的概率为0.95,这时三次同时不发生Ⅰ类错误的概率就为0.95的三次方等于0.857,总体的检验水准就为1-0.857=0.143。该值明显大于0.05,所以在多个均数的两两多重比较时不可采用t检验直接进行。对于多个均数的多重比较目前已经比较成熟,同样主流的医学统计软件SAS、SPSS等也都提供了相应的多重比较的选择。
但是对于多个样本率的多重比较,虽然国内外有诸多研究,但目前尚无普遍认可的可推荐方法,这也可能是SAS、SPSS等软件中还没有纳入率的多重比较方法的原因之一。目前多个率的多重比较的方法多达20多种,大致可分为四大类:1基于检验的方法,如SNK法、Scheffe法等,SNK法与均值比较过程相似,是将样本率进行反三角转换后再计算;2界值表法,是我国学者提出的,并用蒙特卡洛模拟的方法形成了多重比较的卡方界值表;3调整检验水准法,即采用一定的方法对检验水准0.05进行调整;4复合的方法,如AFDR法等。
本次咱们主要介绍一下,容易学习和应用的单步Bonferroni调整检验水准法,当然对于检验水准的调整不仅是Bonferroni法一种哦。Bonferroni法的基本思想是所有独立的两两比较的检验水准之和为总的检验水准,也就是
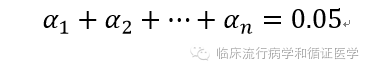
![]()
式中n为两两比较的次数。如果我们将每次两两比较的α都设为一样,那么我们很容易获得新的两两比较的检验水准α’=0.05/n,n为两两比较次数(即)。
举个例子,如果是ABC三组的治愈率的比较,在多重比较时需要进行3次比较,那么其检验水准应该调整为0.05/3=0.0167。一种特殊的情况是,如果仅有AB两组,且对治疗结果仅分为治愈、缓解和无效三种情况,此时需要进行多重比较,分析AB两组的治愈率、缓解率和无效率是否有差别,此时属于构成比的多重比较,其检验水准的的调整方法是α’=0.05/(n-1),n为两两比较次数。因为治愈率 缓解率 无效率=100%。
同样在单因素生存分析的log-rank检验中,研究也需要考虑多组两两比较的检验水准的调整问题。最后需要强调的是多组间两两比较是在总体检验p<0.05的情况下才开展的,如果总体检验多组间无统计学意义,原则上是不应该进行多重比较的。


