这几天,连续碰到多人咨询了两个同样的问题,这两个都是非常有意思的话题:
如何比较两个模型的预测效果?ROC的AUC值比较?IDI、NRI如何计算?
如何做危险因素评分预测模型?怎样将回归系数科学的转换成评分?
这一次,我们聊第二个问题。额,其实,我们要接着聊第一个问题啦。
你知道,ROC评价一致性是有金标准,且结局为二分类指标。当没有金标准,评价的结局还是连续性指标时,用什么呢?就得用Bland-Altman法了!
(二)疑问 连续性指标一致性的判定为什么要用Bland-Altman? 我们有n种方法可以探讨这个问题啊!
我们可以做线性相关,看相关系数是否接近1,是否有意义。
我们可以做线性回归,看截距是否等于0,斜率是否等于1。
我们可以做配对t检验,看两种方法的差值是否等于0。
我们可以算ICC,看其是否接近1。
但是,Bland和Altman说,以上方法都错了!错了!错了!
简单解释如下:
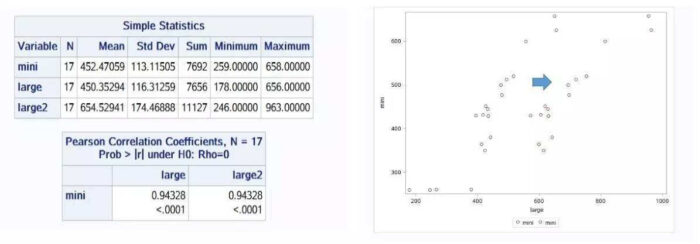
线性相关对系统误差不敏感。也就是说,假如两种方法的测量值是(X, Y),其相关系数为COV(X, Y),我们对第一种测量方法的测量值做一个线性变换:aX b,但其相关系数不变,COV(aX b)=COV(X, Y)。比如,下图中的large2=large1*2-21,但是与mini的相关系数仍然为0.94328,而两种方法的测量值的差异已经是原来的100倍了。从散点图形上看,感觉就是做了拉伸。
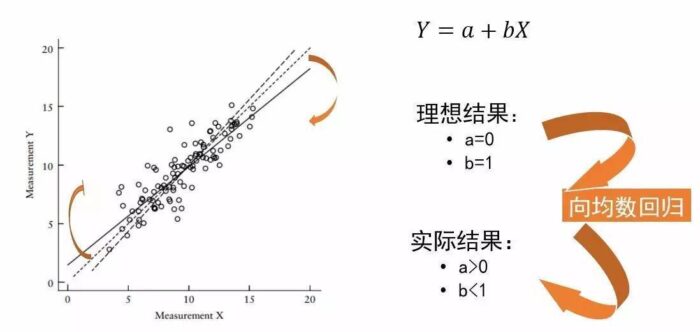
线性回归,即使是两个相等的测量值X,Y,无论谁对谁做回归,总是截距a>0, 斜率b<1,也就是回归线的低端总是被往上抬了抬,顶端总是被往下压了压。对于此,最通俗的解释就是「向均数回归」的作用。
什么是向均数回归?
就是孩子的身高介于父母之间。不然,高的找高的生高的,矮的找矮的生矮的,人类的身高早就两级分化 了。事实去没有,就是因为「向均数回归」啊。
配对t检验,和线性相关不同,她只对系统误差敏感。对于i仪器测量研究对象j的值Xij我们可以拆成三部分:真实值Tj,仪器的系统误差Mij,仪器的随机误差eij。配对t检验的差值d的均值只与系统误差Mij有关,与随机误差eij无关。

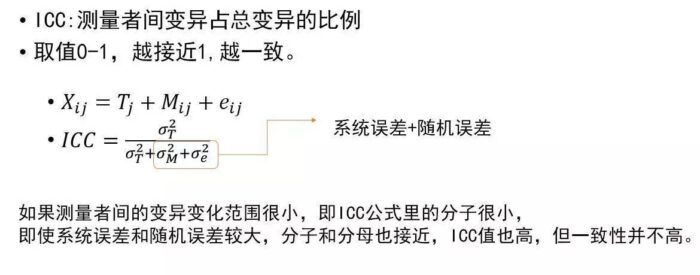
ICC,组内相关系数,是指测量者之间的变异占总变异的比例。其实是一个间接指标。其思路是总变异就那么多,如果测量者间的变异几乎占满了总的变异(ICC->1)的话,那么测量仪器的变异就很小很小了,一致性就很好。但问题是,测量者间的变异有可能相对测量仪器的变异和随机误差之和的变异很小,此时,即使测量仪器的变异很大,ICC也接近1。
看明白了吗?
一张PPT再总结一下。

OK,明白了。那我要学Bland-Altman法。
(三)正戏 Bland-Altman法是什么个东东?简单来说,是Bland和Altman两位生物统计学家于1986年提出的,用两种测量仪器/方法测得值的均数,差值均数及其95%一致限(limitsof agreement, LoA),并配合图示来做一致性评价的一种方法。
以题图为例,横轴为测量值的均数,纵轴为测量值差值的均数,并以1.96倍标准差做出上下限(也称一致限)。如果这个一致限的宽度在临床上可以接受,我们认为一致性较好,否则,一致性差。
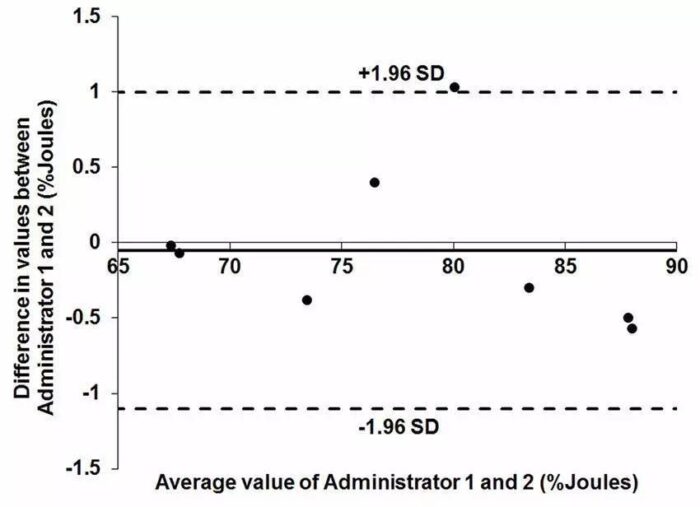
这个图怎么画?
好画,Prisma, MedCalc都有现成的。
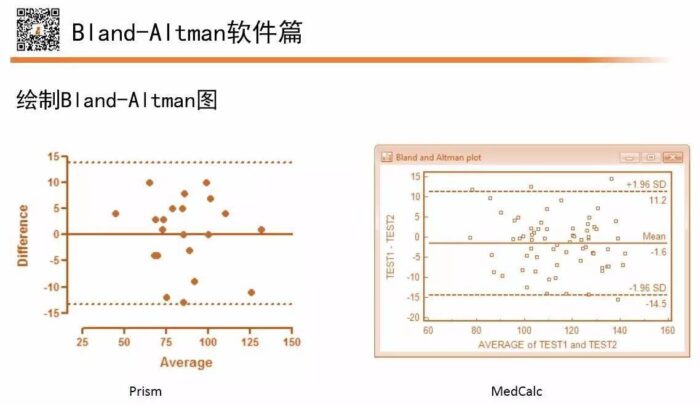
不过,以上的图都没有考虑抽样误差。所以需要给95%LoA加上置信线。我个人喜好用SAS。
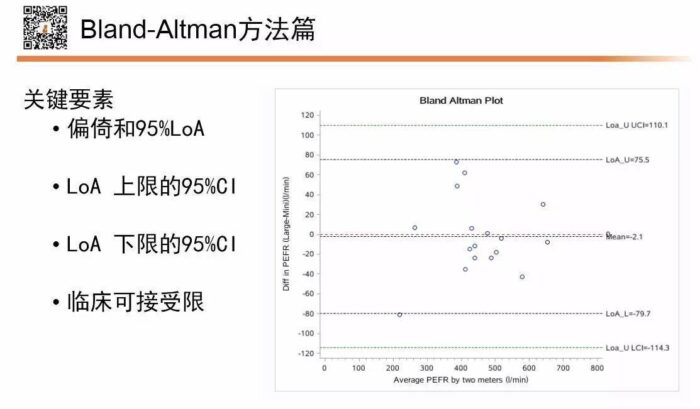
至此,一个同时考虑随机误差和系统误差,同时又可以结合临床意义的形象,直观,简单,方便的连续性指标一致性评价方法就基本讲完了。
(四)后戏 当然,具体在实施时,我们还要对数据进行判定:
是否符合比例偏倚?
是否方差齐性?
是否差值正态?
当数据不符合时,我们需要做log转换,或者改差值为比值,或与均值的比例作为Y轴等。
当然,还有其他一些问题,在实践中仍然值得探索,比如样本量,比如重复测量等等。

最后,八卦下这俩个基友的故事。这俩个家伙在1972年相识于St Thomas' Hospital,后来成了一生的好伙伴。两人最为有名的就是1986在Lancet上发表他们的,一个同时考虑随机误差和系统误差,同时又可以结合临床意义的形象,直观,简单,方便的连续性指标一致性评价方法。后来这种方法便被成为Bland-Altman法。Bland-Altman法方法因其简单,直观,易用,发表后,大受临床大夫欢迎。
那是当然,34026次引用那不是盖的。

此外,Bland和Altman也一直努力普及统计教育,他们合作在BMJ上持续多年,撰写了63篇统计笔记的,篇篇经典,这情怀和友谊也不是盖的。



