1、为什么要进行正态性检验?
正态性检验主要用于判断计量资料是否服从或近似服从正态分布。因为很多常见的统计学方法都要求数据满足正态性,如常见的t检验、单因素方差分析等。在考虑采用上述方法时,要对数据进行正态性检验。
如果数据明显不服从正态分布,但由于我们没有正态性检验的结果,直接使用了t检验、单因素方差分析等参数检验的方法,有可能导致统计效能下降,导致假阴性风险增加。
2、怎么进行正态性检验?
一般可通过图示法或统计学检验法进行正态性检验。常见的统计学检验有Kolmogorov-Smirnov检验(KS检验)和Shapiro-Wilk检验(SW检验),当检验结果的p值小于0.05,则认为数据不满足正态性;反之,则认为数据满足正态性。但需要注意的是,上述检验方法存在一定局限性。
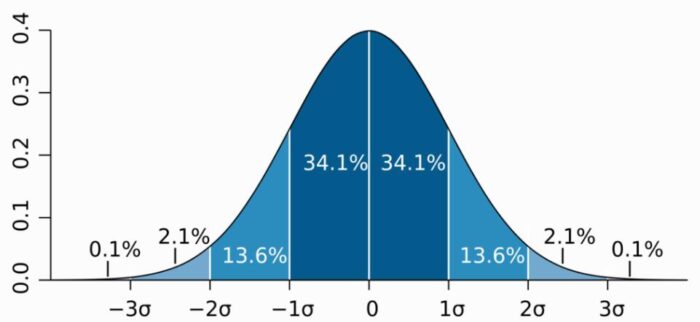
因此,我们常建议研究者通过绘制直方图、QQ图等来判断数据的正态性。在直方图中数据呈现钟型分布,中间高,两端逐渐下降左右两侧呈现对称或近似对称,或者在QQ图中的数据点和理论直线基本重合,则可认为数据满足正态性。但图示法存在主观性的问题,遇到一些不确定的情况,大家可以咨询统计学专家。
需要提醒大家一点,如果是多组间的比较,我们需要分组考察正态性,只要其中一组不满足正态性,就不适合用参数检验了。
3、样本量足够大,是不是就可以不做正态性检验了?
有些读者说,不用这么麻烦,只要样本量足够大,就可以默认数据满足正态性了。这种认识当然是不对的。这种观点的起源是因为对中心极限定理的误解。事实上,中心极限定理说的是:不管总体数据的分布是什么样的(可能是正态,也可能偏态),如果从总体中多次抽样,对于每个抽样样本计算统计量(如均值、中位数)。当每次抽样例数足够大,样本的均值或中位数近似服从正态分布。并不是说:样本量足够大,这个样本就服从正态分布。
4、为什么有些人看一眼,就说我的数据可能不正态呢?
上面说正态性检验的步骤还是有点复杂的,但是为什么有些人只看到数据的均值和标准差,就很有信心的怀疑我的数据不服从正态分布呢?这是因为,统计学家进行了很多模拟,发现对于大于零的数据,如果均值小于标准差,或小于2倍或3倍的标准差,这个数据很有可能不服从正态分布。所以,有些审稿人看到20±35这样的数据,就会怀疑数据的正态性问题。这样,您是不是也学到一招,以后看一眼也能大致判断数据的正态性了。这种经验主要用于对二手数据的粗略判断,对于原始数据还是要通过图示法进行正态性检验。
5、数据不满足正态性检验,有哪些处理方法?
正态性检验那么重要,但是我的数据就是不服从正态分布怎么办呢?这个问题统计学专家在很久之前已经发现并提出了行之有效的方法。比如,我们可以采用非参数检验。如用于两组独立样本的Mann-Whitney U test,多组独立样本的Kruskal-Wallis test。或者,我们也可以做一些数据转换,如对数转换,使得转换后的数据服从正态分布,从而继续采用参数检验。


