与参数检验相比,非参数检验具有检验条件宽松、对样本数据要求较低、计算相对简单的优点。SPSS提供的非参数检验方法较多,包括二项检验、卡方检验、两独立样本检验、两配对样本检验、多独立样本检验、多配对样本检验、游程检验和单样本K-S检验等八种检验方法。
Kruskal-Wallis秩和检验属于多个独立样本的非参数检验,用于在总体分布未知的情况下检验多个样本是否来自于相同分布的总体。Kruskal-Wallis H检验是Mann-Whitney U检验法的扩展,是一种推广的评价值检验。其基本思路是,首先对所有样本合并并且按照升序排列得出每个数据的秩,然后对各组样本求平均秩。如果平均秩相差很大,则认为两组样本所属的总体有显著差异。
以SPSS教程为例:
假设:H0: 不同地区的儿童,身高分布是相同的
H1: 不同地区的儿童,身高分布是不同的
不同地区儿童身高样本数据如下所示:
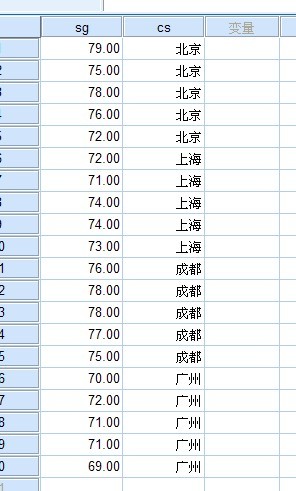
提示:此样本数为4个(北京,上海,成都 ,广州)每个样本的样本量(观察数)都为5个
即:K=4>3 n=5, 此时如果样本逐渐增大,呈现出自由度为K-1的平方的分布,(即指:卡方检验)
点击“分析”——非参数检验——旧对话框——K个独立样本检验,进入如下界面:
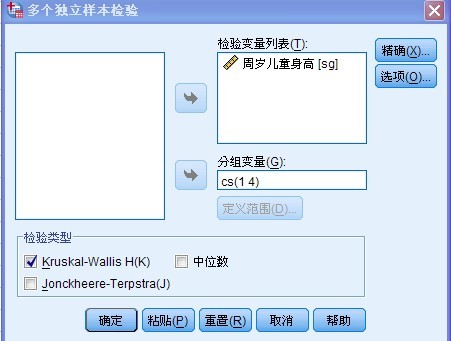
将“周岁儿童身高”变量拖入右侧“检验变量列表”内, 将“城市(CS)变量” 拖入“分组变量”内,点击“定义范围” 输入“最小值”和“最大值”(这里的变量类型必须为“数字型”)如果不是数字型,必须要先定义或者重新编码。
在“检验类型”下面选择“秩和检验”( Kruskal-Wallis检验)点击确定
运行结果如下所示:
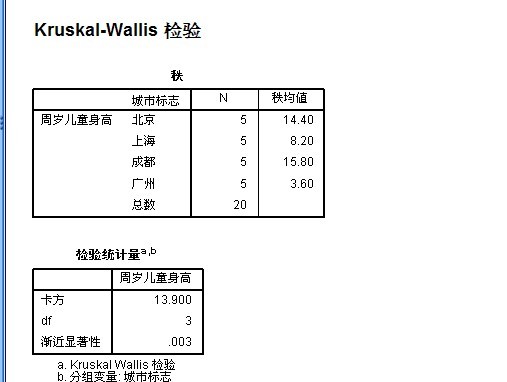
对结果进行分析如下:
1:从“检验统计量a,b”表中可以看出:秩和统计量为:13.900
自由度为:3=k-1=4-1
下面来看看“秩和统计量”的计算过程,如下所示:
假设“秩和统计量”为 kw 那么:

其中:n 1/2 为全体样本的“秩平均” Ri./ni 为第i个样本的秩平均 Ri.代表第i个样本的秩和, ni代表第i个样本的观察数)
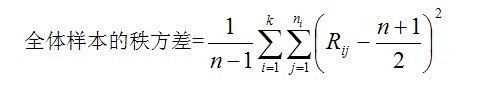
最后得到的公式为:

北京地区的“秩和”为: 秩平均*观察数(N) = 14.4*5=72
上海地区的“秩和”为:8.2*5=41
成都地区的“秩和”为:15.8*5=79
广州地区的“秩和”为:3.6*5=18

接近13.90 (由于中间的计算,我采用四舍五入,丢弃了部分数值,所以,会有部分误差)
2:“检验统计量a,b”表中可以看出:“渐进显著性为0.003, 由于0.003<0.01 所以得出结论: H1: 不同地区的儿童,身高分布是不同的


