统计学中的P值到底是什么意思?2019年3月20日,Nature发表了题为Scientists rise up against statistical significance的评论[1],在学术界又一次引起了对于P值以及零假设显著性检验(NHST,Null Hypothesis Significance Testing)的大讨论。
在过去的几十年间,P值作为统计分析的一条“黄金准则”,其标准和应用一直存在着争议。2015年2月,Basic and Applied Social Psychology(《基础与社会心理学》)宣布了对于NHST的全面禁令[2],要求在此期刊发表的全部文章删除包括P值、置信区间、检验统计量在内的一系列统计分析工具。2016年6月,作为对于争议的回应,美国统计学会(American Statistical Association)发表了题为The ASA's Statement on P-Values: Context, Process, and Purpose的声明[3],以澄清对于P值在实际应用上的误解。
正如上述声明中提到的,在学术界存在着广泛的对P值以至统计分析方法的误用,一刀切地否定甚至禁用P值是过激的。本文旨在对P值做一个简略的科普,希望能够对从事临床和基础研究的朋友们有所帮助。
1. P值以及所有统计分析方法的前提,是良好的实验设计及数据采集过程,以保证样本数据具有很好的群体代表性。统计分析的核心是以随机样本推断整体。例如在临床试验中,如果只考虑到男性患者而没有考虑女性患者,那么无论采用多么高级的统计分析方法都不能对女性患者做出可靠的结论。又比如在药物实验中,如果实验组和对照组不仅在药物使用上有差异,还引入了其它的混淆变量(例如不同的护理条件等),那么同样很难做出可靠的结论。
2. P值是错误率,具体来说是用NHST框架下特定的统计分析方法,在特定的假设下,做出错误结论的概率。
1)在NHST的框架下,对于一个科学问题,需要预先设立两个相反的假设,一个叫零假设,代表“无事发生”,与之相反的叫备择假设。比如,科学家想要研究一种新型降压药是否比传统药物效果好,那么“新药和传统药没什么区别”是零假设,“新药比传统药效果好”是备择假设。又比如,科学家想要研究肺癌的发病率是不是受到大气污染的影响,那么“大气污染不影响肺癌发病率”是零假设,而“大气污染影响肺癌发病率”是备择假设。值得注意的是,在随机性存在时,理论上没有办法同时避免所有错误,这时需要在两种假设中预设一定的倾向。
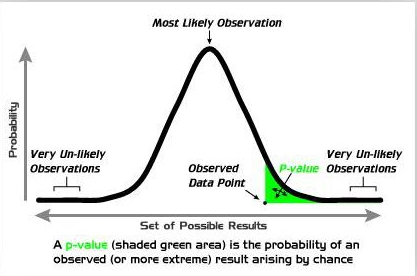
2)P值的原理类似于法律上的无罪推定,即默认零假设(无罪),只在足够证据存在时才转而选取备择假设(有罪)。换句话说,结论为备择假设(有罪)时,这个结论是可靠的,犯错误的可能是很小的,这种很小的可能性就是P值。在这样的原理下,P值只衡量一类错误,即“零假设是真的,但错误地选择了备择假设”,这种错误在统计上又叫“第一类错误”。我们经常使用的“P值小于0.05”的要求,就是为了把第一类错误的概率控制在5%以内。相应的,统计上的“第二类错误”,即“备择假设是真的,但错误地默认了零假设”,却没有被P值计算。
理论上“第一类错误”和“第二类错误”的概率存在此消彼长的关系,无法同时被控制。在NHST框架下,由于只控制了“第一类错误”,“第二类错误”的概率无法被控制,“默认零假设”的结论都是不可靠的。回到降压药的例子,零假设显著性检验默认新药没什么优势,所以,当P值很小时,做出新药有优势的结论是可靠的。而当P值较大时,严格来说只能说没找到足够的证据来证明新药有优势,而不能说新药一定是没有优势的。
3)P值的大小仅仅代表错误率,并不代表结论的强弱。比如,当新药相比传统药的效果只有万分之一的优势时,同样可能得到很小的P值。
4)P值本身就是大量可重复性实验中的个例代表,极小的P值也并不代表结论就是可重复的。以通常所用的0.05(5%)为例。假定新药确实没什么优势,如果世界上有无数家医院在进行着完全相同的平行临床实验,应用相同的统计分析方法,那么每100家医院中,就有5个会得到小于0.05的P值以致得到错误结论。在通常的一次临床实验中,即使得到了很小的P值,也可能就是碰巧。
5)P值对应着特定统计分析方法和其自然存在的模型假设。我们通常所用的t检验,卡方检验,F检验等等,都有不同的模型假设。只有数据符合模型假设时,P值才是有意义的。比如在比较多个实验组之间的药物效果时,可以使用方差分析(F检验)。但是方差分析要求每组数据都符合正态分布,否则P值就不是正确的错误率了。每种假设方法对应的模型假设,以及如何判断数据是否符合假设,都需要更加系统的统计训练。
6)P值小于0.05的标准只是为了方便,意思是0.05的错误率是可以接受的,除此之外没什么深层意义。
3. 在科学研究上,如何应用P值需要具体问题具体分析。以下是一些需要注意的方面:
1)计算P值之前,应该首先判断实验是否合理,样本是否具有代表性,是否用对了统计方法等,在有条件的情况下应该尽量咨询统计专业人士。
2)禁用P值是不可取的,其后果是放弃对于科学研究中错误的控制,这显然是不严谨的。
3)P值的标准应该根据需要放宽或收紧。
4)即使得到了很小的P值,为了进一步验证结论的可靠性,仍然应该进行多次重复实验。
作者介绍
郝涵,2011年于清华大学取得数学学士学位,2016年于宾州州立大学取得统计学博士学位,现为北德州大学数学系助理教授。Department of Mathematics, College of Science, University of North Texas.
参考文献
[1] Amrhein V, Greenland S, McShane B. Scientists rise up against statistical significance. Nature 2019;567:305-7.
[2] Trafimow D, Marks M. Basic Appl Soc Psych 2015;37:1-2.
[3] Wasserstein RL, Lazar NA. The ASA's statement on P-values: context, process, and purpose. Am Stat 2016;70:129-33.


