一 、定义及理论
多重共线性是指线性回归模型中的解释变量之间由于存在高度相关关系而使模型估计失真或难以估计准确。
对线性回归模型Y=β0 β1X1 βnXn ε,公式表示n个解释变量的变化引起被解释变量 Y 的线性变化,其中被解释变量 Y 为n维向量,自变量 Xi为 n×p 阶矩阵,β0是常数项系数,βj为回归系数,ε为随机误差向量。基本假设之一是自变量X1、X2……Xp之间不存在严格的线性关系。如不然,则会对回归参数估计带来严重影响。
对于解释变量X,如果存在一组不全为零的数λ0、λ1、λ2……λn,使λ0 Xi0 λ1Xi1 λ2Xi2……λnXin=0,则称线性回归模型存在完全共线性;如果还存在随机误差m,满足Em=0,E㎡<∞,使得λ0 Xi0 λ1Xi1 λ2Xi2……λn Xin m=0,则称线性回归模型存在非完全共线性。如果线性回归模型存在完全共线性,则回归系数的LS估计不存在,因此,一般情况下在线性回归分析中所谈的共线性主要是非完全共线性。 解决共线性的方法主要有:排除引起共线性的变量,找出引起多重共线性的解释变量,将它排除出去,以逐步回归法得到最广泛的应用;差分法,时间序列数据、线性模型:将原模型变换为差分模型;减小参数估计量的方差:岭回归法。 二 、产生的原因
经济变量相关的共同趋势、滞后变量的引入、样本资料的限制
三 、造成的影响
第一、完全共线性下参数估计量不存在;第二、近似共线性下OLS估计量非有效;第三、参数估计量经济含义不合理;第四、变量的显著性检验失去意义,可能将重要的解释变量排除在模型之外;第五、模型的预测功能失效。
四 、检验和处理多重共线性的方法
1 逐步回归法(Stepwise Regression)
逐步回归法是目前应用比较广泛的一种共线性检验方法,它的前提假设是自变量之间不存在共线性。它的原理是:以Y为被解释变量,逐个引入解释变量,构成回归模型,进行模型估计。根据拟合优度的变化决定新引入的变量是否独立。如果拟合优度变化显著,则说明新引入的变量是一个独立解释变量;如果拟合优度变化很不显著,则说明新引入的变量与其它变量之间存在共线性关系。它的运行过程是:首先采用向前选择的方式选择第一个变量,若不满足标准则终止选择,按偏相关系数选择下一个。同时,根据向后剔除的标准,考察已经进入方程的变量是否应该剔除,直到没有一个变量满足移出标准,为防止变量重复进入和移出,F-进入判据必须大于F-剔除判据。
2 岭回归法(Ridge Regression)
岭回归又称脊回归、吉洪诺夫正则化(Tikhonov regularization),是一种改良的最小二乘估计方法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。它的估计量为β^(k)=(X′X kI)-1X′Y,其中 k>0 且为常数。当出现高度共线性时, 通常认为岭回归估计的参数比用普通最小二乘法(OLS)估计要好。
3 主成分回归法(Principal Components Regression)
主成分回归是以主成分为自变量进行的回归分析,基本步骤:(1)将自变量转换为标准分;(2)求出这此标准分的主成分,去掉特征根很小的主成分;(3)用最小二乘法作因变量对保留的主成分的回归;(4)将回归方程中的主成分换成标准分的线性组合,得到由标准分给出的回归方程。 操作过程
由于各种方法的使用范围和同学们的接受程度,这里主要对逐步回归法进行详细介绍,岭回归方法只进行简单的操作过程描述,而主成分回归实现过程比较复杂,需要用到Descriptives、Data Re-duction、Linear Regression、Compute Variable等模块的功能,过程比较复杂,不再介绍,这里在文后贴了几篇参考文献,感兴趣的同学可自行查阅学习。
1 逐步回归法(Stepwise Regression)
基本过程是:分析——回归——线性,下面我们详细介绍:
打开要分析的数据,这里我们直接进入到“回归分析”页面框:选好自变量和因变量,如图所示,然后进行参数的详细设置。主要是“统计量”部分,进入统计量按钮,看到图中右下角所示对话框。其中,“估计”和“模型拟合”是默认选项,其他参数按需选择,但是我们必须要选择的是“共线性诊断”,也可以选中“描述性”,这里可以输出各变量间的相关系数,点击继续。其他所有选项可以默认。因为我们是逐步回归法,数据进入的方法上,我们选择“逐步”。然后,点击“确定”,运行数据,输出结果。
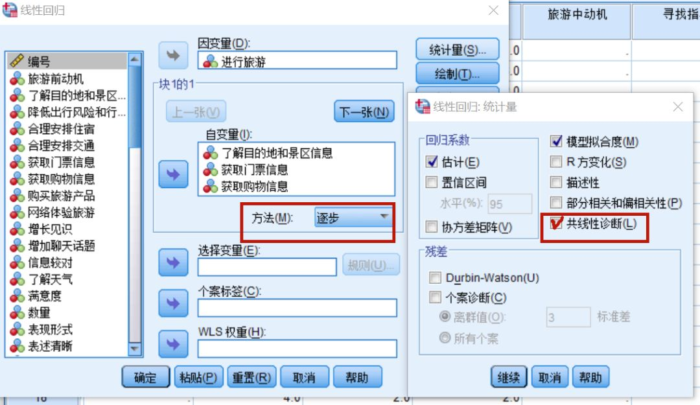
下面我们来看结果:输出结果的表格很多,我们不一一列举,这里只看能诊断共线性的相关表格:
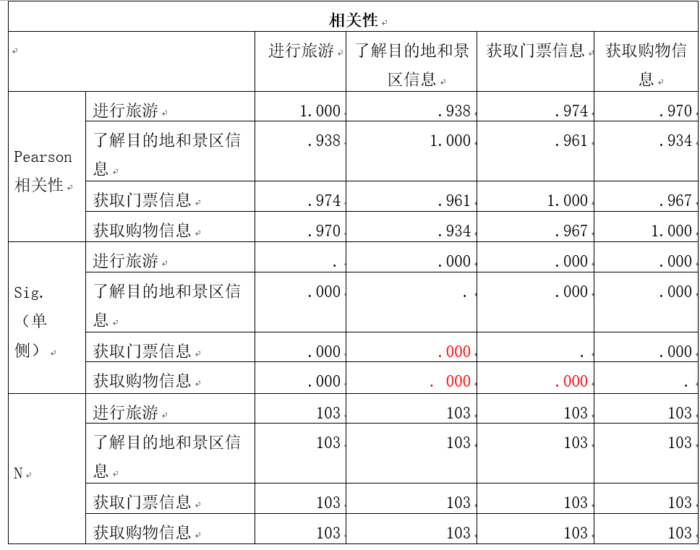
首先来看相关系数表格,在这里可以检验各自变量之间是否存在共线性:在结果输出表格中,显示了所有变量两两之间的Pearson相关系数及其对应的P值,一般认为相关系数 > 0.7可考虑变量间存在共线性。本案例结果显示:自变量之间相关系数均 > 0.7,且P值均 < 0.05,表明自变量间相关性较强,说明自变量之间存在共线性。
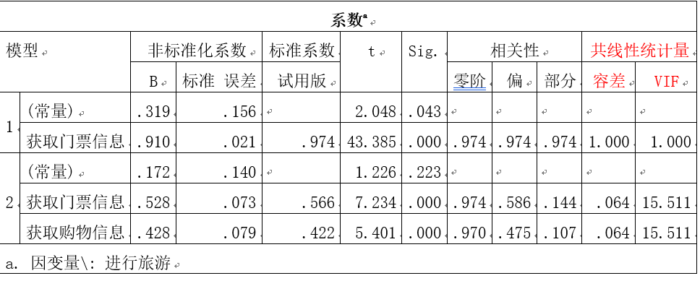
接下来是“回归系数表”,如图所示,表格里显示了共线性诊断的两个统计量:Tolerance(容忍度)和VIF(方差膨胀因子)。一般认为如果Tolerance < 0.2或VIF > 10,则要考虑自变量之间存在多重共线性的问题。案例中各自变量的Tolerance均< 0.2,VIF均 >10,表明自变量之间可能存在共线性,此结果与相关系数表格结果相同。
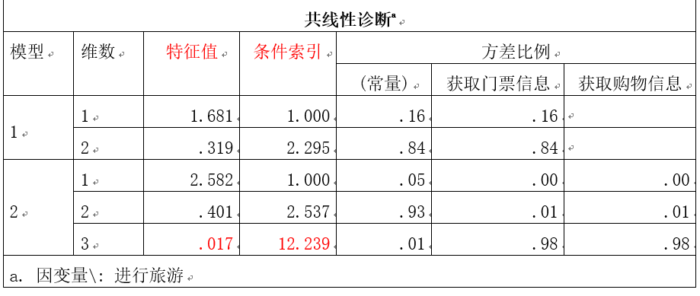
然后,需要我们关注的是共线性诊断表格,这里需要看这两个参数:特征根和条件指数。多个维度的特征根约为0证明存在多重共线性,条件指数大于10时提示我们可能存在多重共线性。我们解读案例结果:我们可以看到,不管是在模型1还是在模型2中,随着往模型中逐步添加自变量,特征根的值逐渐减少而接近0,条件索引的值则随着自变量的加入而逐渐增大。这个变化在模型2中非常明显:在加入自变量3后,特征根接近于0,特征值超过10。结果表明变量间可能存在多重共线性。
2 岭回归法(RidgeRegression)
岭回归有两种操作,一种是像逐步回归一样的简单操作,一种是语法操作。
我们先来看简单操作:这种操作对现在版本的SPSS基本都能实现(SPSS18.0以上版本都可以实现),操作过程是“分析——回归——最佳尺度——规则化”如图所示。
语法操作:文件——打开——语法,找到你的SPSS安装的路径(安装到哪个盘里了),按照“SPSS安装目录SPSSStatistics22SamplesSimplified ChineseRidge regression.sps”,调用语法并运行。
好了,关于多重共线性的介绍,到此全部结束,祝大家学习快乐。
参考文献:
[1]鲁茂.几种处理多重共线性方法的比较研究[J].统计与决策,2007(13):8-10.
[2]蔡素丽.多元线性回归模型应用实证分析[J].廊坊师范学院学报(自然科学版),2017,17(04):5-8.
[3]张钊.利用主成分法减小多重共线性影响的实证分析[J].兴义民族师范学院学报,2017(05):109-113.


