我们知道logistic回归的模型是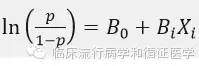
,而log-binomial回归只将模型作一点变化,即将p/(1-p)换成p(p为结局发生的概率)。模型很容易理解,但模型等号前的lnp是个负数,而等号后面的B0 BiXi可以为正也可以为负,因此在回归时需要加一个限制条件即B0 BiXi≤0,因此log-binomal回归是一个有偏估计。
现在我们模型一个数据看看两个回归的结果。我们设定某病的基线患病率为10%,分别模拟RR=1,2,3的三个数据,总人数为1000,暴露组和非暴露组各500例。如下表。当RR=1时,暴露组和非暴露组各有50人患病。

分别使用logistic回归和log-binomial回归进行统计分析,得到的结果如下表。
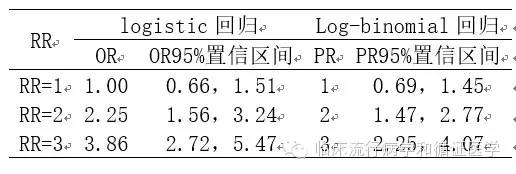
可以看出,虽然log-binomial回归是有偏估计,但估计值与预设的RR完全一样,而且置信区间也比较小,也即更加精确。因此当结局发生率较高,应该用log-binomial回归尝试进行统计分析。
在进行log-binomial回归时,自变量如果是连续变量时,可能造成模型不收敛,因此我们需要将数据进行加权,方法是将原数据复制后,复制数据其它不变,将结局变量0与1对换,给予原数据较高的权重(一般0.99)以上,给予复制数据较低的权重(一般0.01以下),再进行回归分析。log-binomial回归尚不能在SPSS菜单中实现,现把程序给大家,拿走不谢。
proc genmod data=a;
ods select ParameterEstimates;
ods output ParameterEstimates=para0;
weight w;
model y=x/D=BIN link=LOG INterCEPT=-1LRCI;
run;
proc print data=para0;
run;
data para;
set para0;
PR=EXP(Estimate);
LPR=EXP(LowerLRCL);
UPR=EXP(UpperLRCL);
keep Parameter PR LPR UPR;
proc print data=para;
run;


