近日有医院的小伙伴问起岭回归分析的SPSS操作,在此与大家一起复习一下。
岭回归分析(Ridge Regression)是一种改良的最小二乘估计方法,它是用于解决在线性回归分析中自变量存在共线性的问题。什么?共线性是什么?共线性就是指自变量之间存在一种完全或良好的线性关系,进而导致自变量相关矩阵之行列式近似为0,导致最小二乘估计失效。此时统计学家就引入了k个单位阵(I),使得回归系数可估计。设么?没看懂,那就算了。
知道岭回归分析就是用来解决多重共线性的问题,就够了。在医学科研的实际工作中,往往不需要创造算法,会用算法就行。当然如果你有心研究其原理,那更是极好的。
下面我们还是通过实例来学习岭回归分析的应用条件和SPSS实习方法吧。用SPSS自带的例子(来自SPSS 20.0版的示例数据库,其他版本的就别找了),某研究者想了解B超下胎儿的身长、头围、体重与胎儿受精周数之间的关系,即B超测得上述参数之后,用它们来推测胎儿的受精时长(周数)。我们很容易想到用多重线性回归来解决,以胎儿周数为因变量,以身长、头围和体重为因变量,做回归之后我们发现,结果如下:
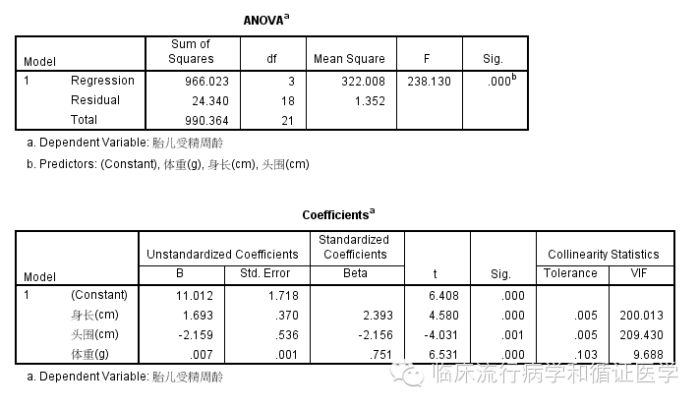
不会吧?!头围尽然与周龄成负相关,开玩笑啊。这个方程肯定是有问题,细心的读者也已经发现方差膨胀因子(VIF)大到200多了(VIF是用来判断自变量共线性的一种方法,如果大于10即认为存在较为严重的共线性)。现在该怎么办?岭回归该发挥作用了。
岭回归分析在SPSS中没有可供点击的对话框,我们需要写一段超级简单的语法来调用SPSS的宏。SPSS公司可能也觉得羞愧,没有提供人机交互的对话框,于是他们提供了一段宏程序,存储路径为“你的SPSS安装目录SPSSStatistics22SamplesSimplified ChineseRidge regression.sps”。
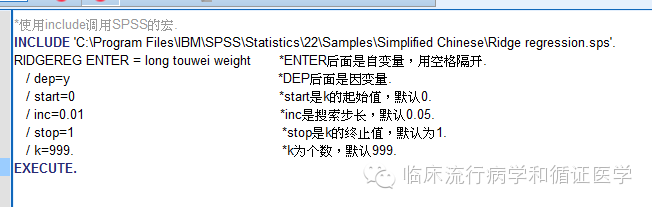
我们在做岭回归分析时,只需要调用它就行,调用语法如下(*后面是注释):
什么?你调用不了?哦,那是因为你没有SPSS目录下的修改权限。什么是修改权限?这是电脑问题,Windows为了保护其程序文件,一般默认不给用户修改权限,需要用户自己去改,至于怎么改自己问百度吧。
进行上述运算后,你会得到如下几个结果:1、不同K值下自变量的标准化回归系数;2、岭轨图,3、R方的变化图。
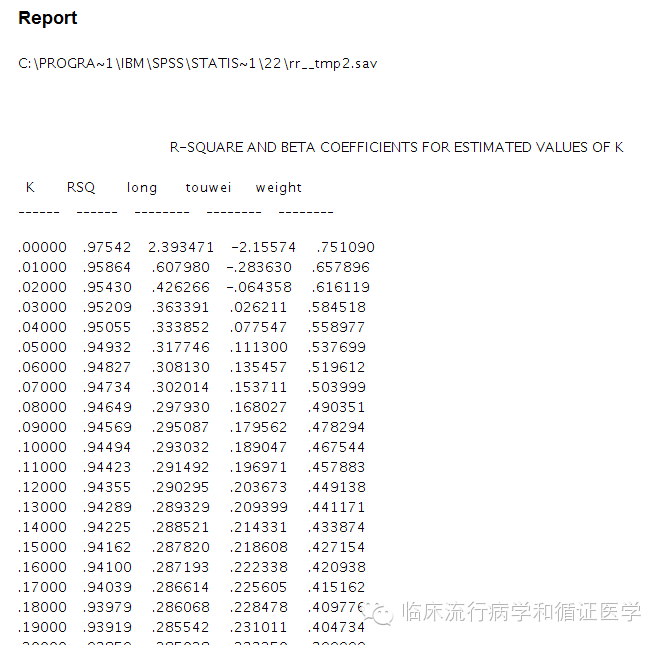
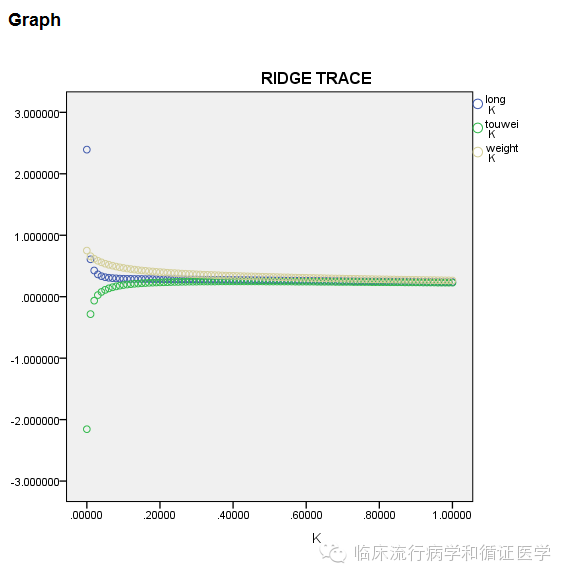
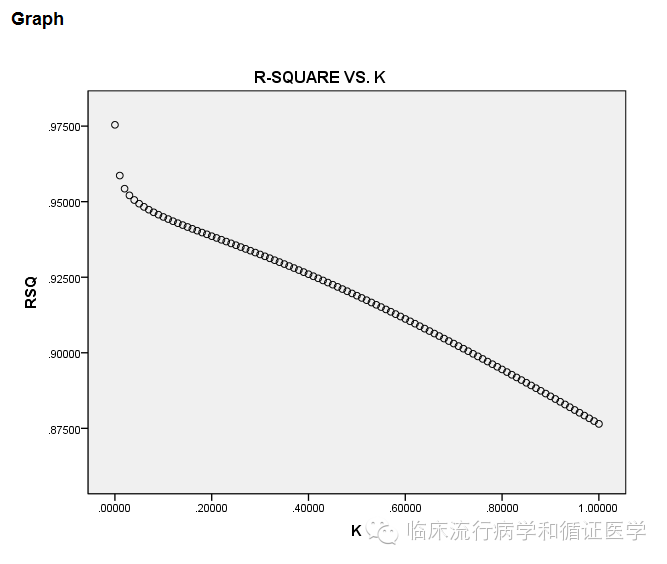
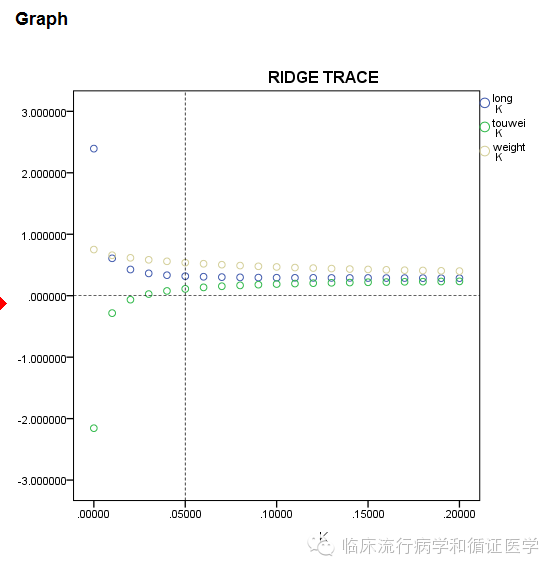
如何选择结果呢?我们需要选择一定K值下的标准化回归系数,选择的原则是各个自变量的标准化回归系数趋于稳定时的最小K值。因为K值越小我们引入的单位矩阵就少,偏差就小。有同学说上图看不起,那么我们把岭迹图放大如下,就可以看出k大约在0.05时,各个自变量的标准化回归系数就趋于稳定了。

有了上述的结果,我们就获得了岭回归的各个自变量的标准化回归系数,也算是做完了。但是有人又问了,我们能不能获得非标准的偏回归系数、t值和p值呢?当然是可以的,但是SPSS原始的宏不提供p值的计算,所以我们需要在SPSS的宏中加入这一句话“. computeppp=2*(1-tcdf(abs(ratio),n-nv-1)).”,这句话就是计算p值的。同时我们对print结果略作修改。这句话加在下图的位置上:

修改完宏之后,再修改上述调用语句,将其中的k改为等于0.05,SPSS就会做k=0.05时的岭回归分析,并给出各个自变量的检验结果,结果如下:
至此完整的岭回归分析就算做完了,各个自变量的标准化回归系数合理多了吧。


