有序多分类变量是很常见的变量形式,通常在变量中有多个可能会出现的取值,各取值之间还存在等级关系。比如高血压分级(0=正常,1=正常高值,2=1级高血压,3=2级高血压,4=3级高血压)、尿蛋白水平(0=-,1=±,2= ,3= ,4= )等等。与无序多分类变量不同,有序多分类变量的各个选项直接呈现向一个方向递增或递减的关系。
当Logistic回归中需要将有序多分类变量代入自变量X时,我们如何处理呢?通常大家会习惯性的将有序多分类变量直接代入。这当然不是不对,但是有个前提条件,就是该有序多分类变量每改变一个单位的时候,结局风险增加倍数相同。
每改变一个等级,对结局贡献相同或相似时
上面的标题听起来不大好懂,但是可以简单的用个例子和图表示一下。比如我们关心研究对象是否接受治疗,也就是研究对象中,有一部分人出现了“接受治疗”这个结局。可能影响结局的变量之一是教育程度。
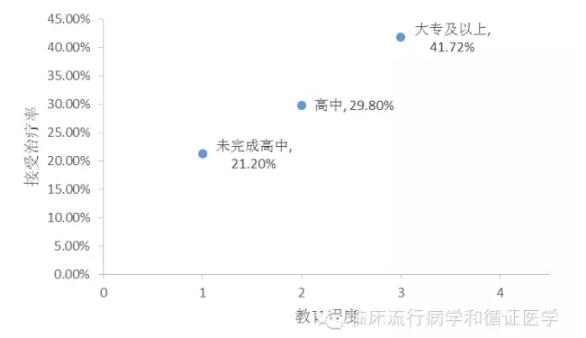
我们看图说话,教育程度每增加1个水平,“接受治疗率”提升的百分比相近。“高中”是“未完成高中”治疗率的1.4倍;“大专及以上”是“高中”治疗率的1.4倍。换句话说也就是教育程度只要提高1个水平,不管从哪一个等级提升,对结局发生概率的影响都是相当的。(当然,在这里我们没有考虑其他因素分布的问题。)
此时我们通常直接把有序多分类变量代入Logistic回归模型,而不对变量进行额外设置。跑出来的结果解读起来也和连续变量差不多。
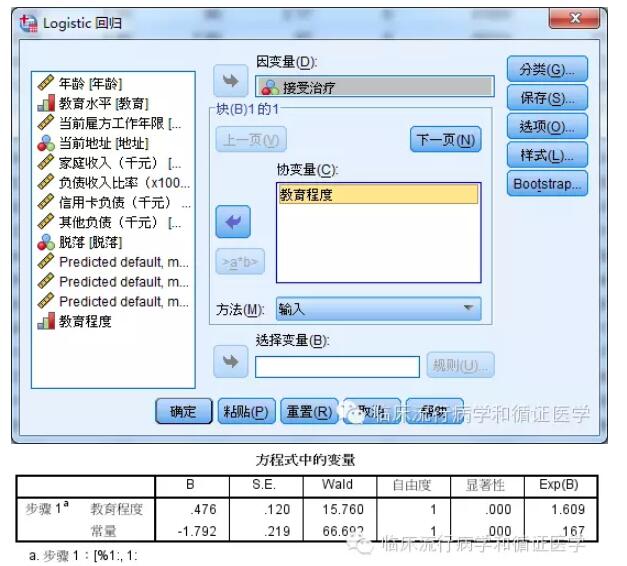
教育程度还是有统计学意义的,我们试着解释一下OR值(Exp(B))。此处,我们认为只要是教育程度相差1级,那么出现“接受治疗”这一结局的概率就增加到1.609倍,相差2级概率就为1.609的2次方倍。
同样间隔的不同等级间,效应不一致时
同样的例子,如果同样相差一个等级,结局发生概率的增加倍数不一样。比如我们把上面的例子改成这样。
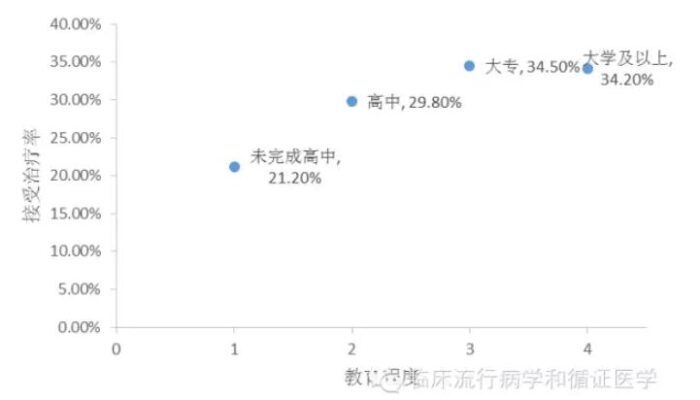
同样是有序多分类变量,从“未完成高中”到“高中”改变了1,结局发生概率升到1.40倍;从“高中”到“大学”改变了1,结局发生概率升到1.16倍;从“大专”到“大学及以上”也是改变了1,结局发生概率升到之前的0.99倍。可见此时每升高一级,接受治疗的发生率提高的倍数并不一致。如果按照最开始的方法直接把多分类变量代入模型,得到的结论就有问题了。
此时,可选的做法有几个,如果在各等级间,临近等级的改变完全不增加结局的风险,则可以简单粗暴的把相近的几个级别合并。
当然还有更细致的办法,就是按照“SPSS:二元Logistic回归中自变量的处理和解读——无序多分类变量的处理”的做法,把有序多分类变量按哑变量处理,各级别都和其中的某一个级别进行比较。过程如下:
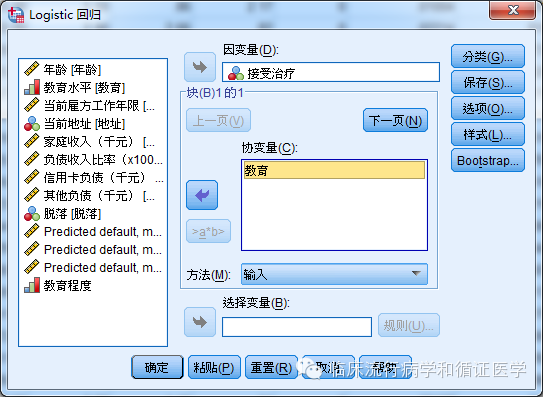
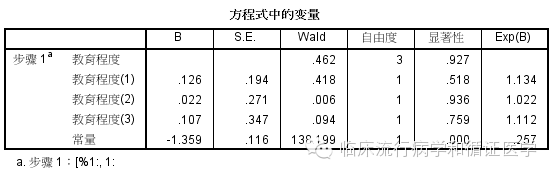
结果解读见“SPSS:二元Logistic回归中自变量的处理和解读——无序多分类变量的处理”。
结果解读方法见“SPSS:二元Logistic回归中自变量的处理和解读——无序多分类变量的处理”。
与结局不成线性关系时,无序多分类变量效应拐点的探索
探索的方法有很多种,首先可以参考的就是我们讲过的连续变量的处理方法,详见“临床研究中年龄只能是连续变量吗?”。
在Logistic回归处理有序多分类变量时,还有更简化的方法,就是在
这个步骤中,选择特定的对比方法。
当在对比中,选择“差值”方法时,会变为如下结果:
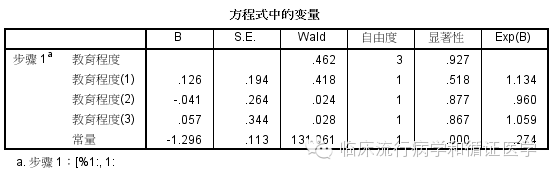
此处每个教育程度水平的OR值不再是和第一个或最后一个水平进行比较,而是直接和前一个水平进行比较。比如“教育程度(2)”对应的OR值为0.96,其含义是指其出现结局事件的概率是“教育程度(1)”的0.96倍。若某个水平的OR值与其他水平OR值相差过多,意味着从临近水平进入这一水平这“1个”改变量,带来的效应与其他水平不一致,提示此处可能为效应的拐点。
我们还可以选择“Helmert”选项,此时每个教育水平为与之前所有水平总体的比较。其他各选项的解释可以参考张文彤编写的《SPSS统计分析高级教程》Logistic回归的章节。


