在logistic回归出现连续变量时应该怎样分析?结合logistic回归的特点,按照实际分析的思路进行进一步阐述。
分析思路的讨论
很多朋友在进行logistic回归分析的时候,遇到连续变量会有两种常见的处理方式:
1、直接将连续变量代入模型。如果从理论上讲,变量与结局的关系确实为简单的线性相关时,确实可以这么做。但是从我们的经验看,多数情况下直接这么操作的话,我们还是会错过很多信息的,详见158期。
2、直接按照临床意义、常规认识划分为二分类(是/否)或有序多分类变量(如疾病分级),看起来似乎比较合理,结果的临床意义也更加明确了(等级之间的变化更容易被临床解释,比如血压从II级升高到III级,似乎比血压升高1kPa的意义更容易理解)。但是使用既定的认识将数据简化,似乎有漏掉了发现新规律的机会。毕竟对于我们自己的数据和人群,未必就是按照常规认识在发生着变化的。
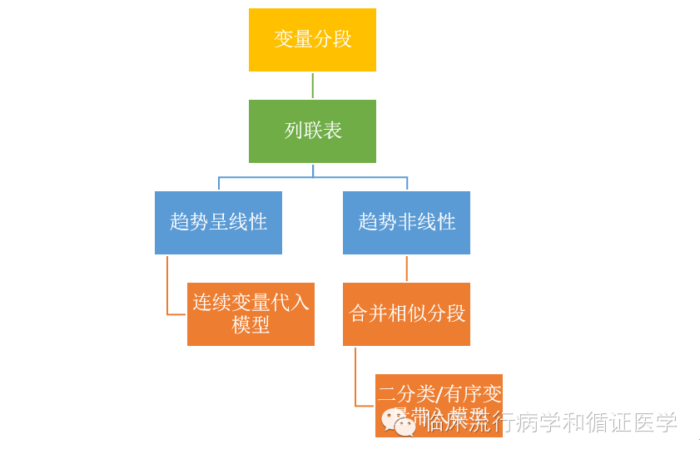
因此,对于连续变量,我们的建议分析思路应该是这样的:一切从认识连续变量与结局变量的关系开始
决定如何对待连续变量,首先需要了解连续变量与结局的关联。
对此,我们通常会尝试将连续变量划分为有序变量,然后在用列联表进行观察。比如在197和200期用到的例子中,我们希望探讨一些变量与患者是否会脱落这一结局的关联。在此,收入水平、年龄、家庭负债率这几个变量是连续变量。
1、让我们先从负债率入手吧。负债率是0-100的数值,暂且让我们以5%为一层,将负债率划分为有序多分类变量看看。
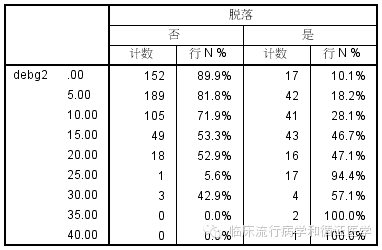
我们看到,随着负债率的增加,患者脱落比例也在持续增加。但是当负债率大于25%的时候,由于每层患者例数都很少,让结果变得不那么稳定了,但是总的来看,还是负债率越高,患者越倾向于脱落的。因此在这里,我们可以首先尝试将25%以上负债率合并为同一层。结果如下:
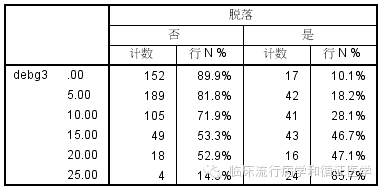
我们来看看随着负债率的升高,间脱落率是如何变化的。
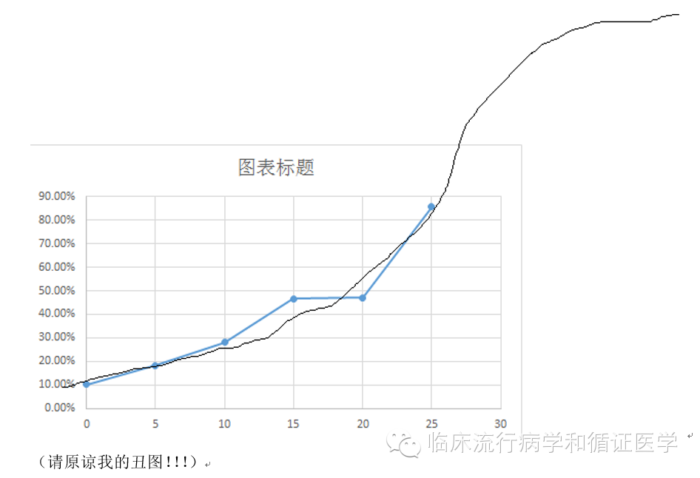
除了15-20这一层,似乎脱落率在每层之间都按照相似的比例增长,近似于logit转换之后的分布。
因此,对于负债这一指标,我们可以作为连续变量直接代入模型。其实更简单的看,如果几个数据点间为等比数列,那么我们就可以将其当做连续变量代入模型,否则就需要做其他考虑了。
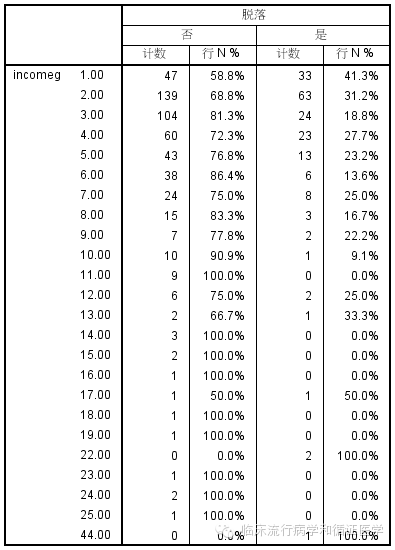
2、接着让我们对收入下手。我们按照1000为一个收入段,将收入变为有序分类变量。1000这个层实在太小了,所以我们会看到很多类别,千万别被吓到。我们同构设定表就可以得到每层中脱落患者的比例。
当我们看到这个表的时候,我们就会发现这样分层似乎并不合理,因为实在是太细了,以至于很多层中只有寥寥1、2个患者,实在无法判脱落断率是如何变化的。但是我们还是可以发现一些线索,从上表中我们可以看出收入的分布,1-6的例数较多,例数分布看上去近似正态分布。同时,从1-6似乎脱落率是在逐渐下降的。
然而从7开始,患者例数极具减少,数据开始变得不那么稳定了。10以上就更少了。所以我们可以先试着把10以上合并为一层,然后再看看规律。
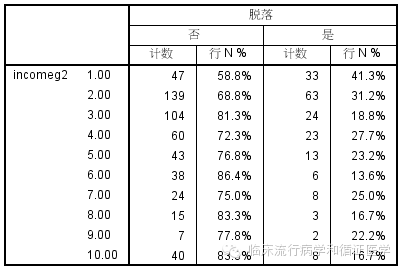
这不,合并之后数据似乎稳定一些了。我们郁闷的发现,似乎脱落率并没有随着收入的增加而持续变化。真实的变化规律是,在1-3随着收入的增加迅速下降,而3以上的收入水平中,脱落率几乎没什么太大变化。
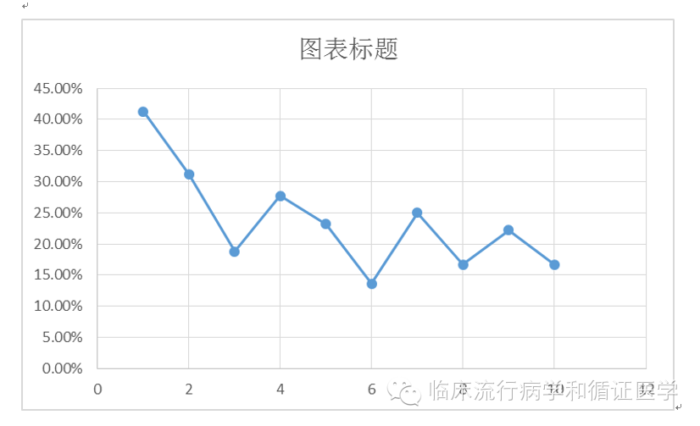
因此,好的做法是将收入这个连续变为有序多分类变量,级别定为3即可。1就是收入1,2为收入2,3则代表≥3的所有收入水平。然后参照200中有序多分类变量的处理方式进行分析。
当然,如果最后分类出来只有两个水平的话,那就当做二分类变量好了。
最后的废话
其实,连续变量虽然信息量很大,但是有时候这些信息量并非都具有临床实际意义。在我们分析的时候,如果一味追求信息量,而忽略了数据背后真实的规律,则会与很多新的发现擦肩而过。正确的做法是先通过最简单的描述来探索连续变量与结局间的可能规律,在进一步进行logistic回归分析进行探讨。
当然,本例子并没能说明所有问题,有的时候由于其他一些因素的作用,改变了自变量与结局间的关系,这时我们可能需要做更复杂的前期分析来初步探讨自变量的效应了。


