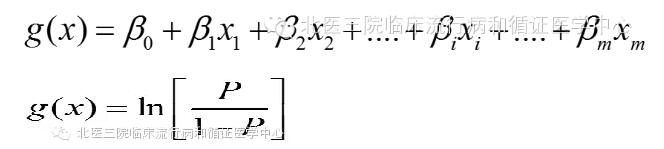
模型参数对结果解读相当重要,其中β0为常数项,β1,β2……。βm分别为m个自变量的偏回归系数。
由上述公式可知,偏回归系数βm表示扣除了其他自变量的影响,自变量xm改变一个单位时logitp的改变量。
知道了Logistic回归的原理,SPSS的操作马上呈现给大家。例:比较新疗法与旧疗法治疗某种疾病的疗效。共40例患者,20例接受新疗法,20例接受旧疗法治疗。根据专业知识,患者的病情严重程度、年龄对疗效也有影响。如何评价新旧疗法的疗效(注:作为举例,本例样本量仅为40例,由于样本量太小,Logistic回归的结论仅作为参考)
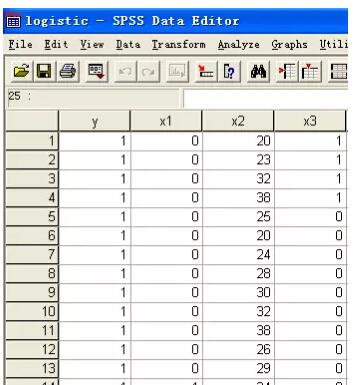
变量说明:Y:治愈情况,1=治愈;0=未治愈;X1:病情严重程度,0=不严重,1=严重;X2:年龄。X3:治疗方法,0=新疗法,1=旧疗法。
执行Analyze-Regression-Binary Logistic
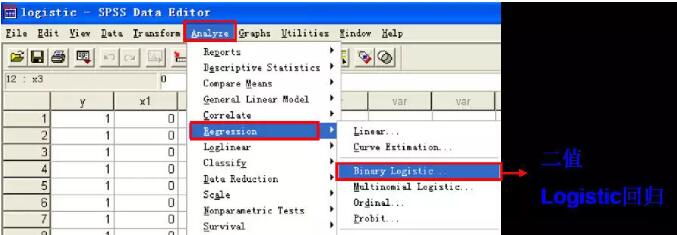
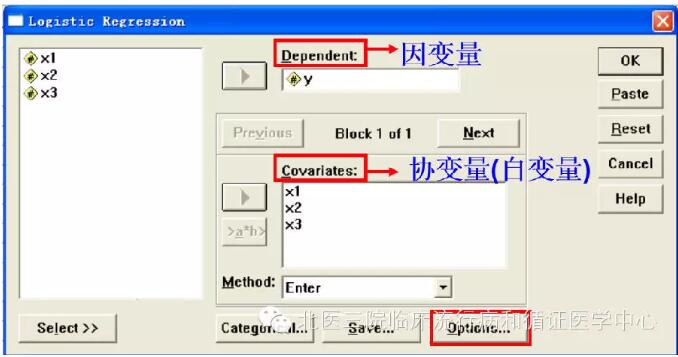
将y选入因变量,x1,x2,x3选入自变量。这里注意一下,当自变量的个数较多时,为了使建立的Logistic回归模型比较稳定和便于解释,应尽可能将回归效果显著的自变量选入模型中,将作用不显著的自变量排除在外。具体方法有前进法、后退法和逐步法(后退法最好),一般默认为Enter(全部进入)。
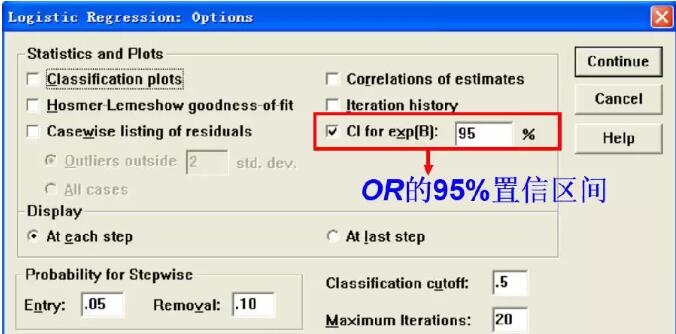
在一系列点击菜单的操作后,我们终于看到了输出结果。首先是对Logistic回归模型的检验。
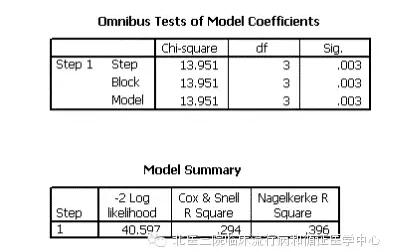
经统计学检验,模型c2=13.951,P=0.003,Logistic回归模型有显著性。
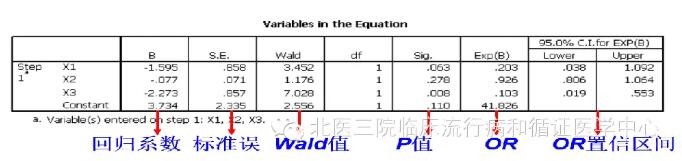
根据模型,病情严重程度与治疗方法对患者的治愈情况有影响;其中病情严重组相对于不严重组,OR=0.203,95%置信区间为(0.038,1.092)(区间包括1,缺乏实际意义,不多作解释);旧疗法组相对于新疗法组,OR=0.103,95%置信区间为(0.019,0.553)。
鉴于Logistic回归的自变量既可以是连续变量,也可以是分类变量。对于连续变量、二分类变量和等级变量无需特殊处理,但如果自变量是名义变量,我们需要将名义变量哑变量化,可通过Categorical按钮来实现。


