顺便提一下,在ICC研究的文献中,上述“同一个概念的不同测量”是被叫做“different variables of a common class”。这里所涉及到的名词,如class,cases, variable(以及可能会出现的measurements, raters, judges, items, objects等等),如果翻成中文、都很容易产生望文生义的误导。我一开始接触有关文献时,也曾迷惑过,后来把ICC的公式(右下)与Pearson r公式(左下)比较一下,就清楚了这些名词的真正含义。所以,我们还是不能不看公式。
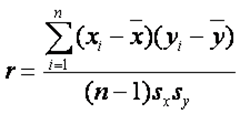
在r的公式中,xi和yi分别是概念X和Y的测量值、和分别是X-和Y-的均值、Sx和Sy分别是X和Y的标准差,n是样本数。(由此可见,X和Y的取值范围可以完全不一样,如X可以是从-1到1而Y可以从0到10000;两者的标准差也由此可以完全不一样。其结果根本不会影响r的值。)而在icc中,为了强调“组内”的意义,我将X改写成X1、Y改写成X2(当然改写前后变量并没有本质区别)。两个公式的真正区别在于均值及标准差的计算,r中的X和Y均值及标准差是分别独立计算的、而icc中的是X1和X2的pooled mean(联合均值)、而也是X1和X2的pooled variance(联合方差、即联合标准差之平方)。由于ICC值是每个观察值减去“联合均值”(而不是各自的独立均值)、加总后再除以“联合方差”(而不是除以各自的独立标准差之乘积),所以其计算结果反映了“组内”的相关系数。(注意,“联合方差”背后有一个更严格的要求,即X1和X2的方差要相等。这一要求不是很容易满足的。如果你的两次测试之间有一定的时间间隔而其中有发生过什么重要的事件,如学校开设了卫生课或召开了运动会,使得学生之间健康行为的差异缩小了或扩大了,那么就不适合用ICC了。)
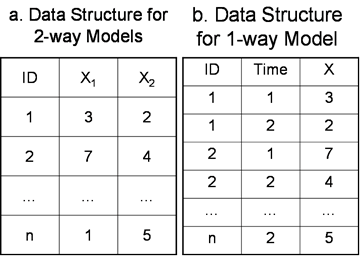
好了,在上述简单背景的基础上,我们来讨论你的问题:如何检验ICC?具体来说,就是如何选择合适的ICC模型。让我们从计算ICC所需要的数据结构说起(右图)。图a是最常见的结构,其中每个row(行)代表一个case(本例是ID从1到n的学生),每个column(列)是同一概念的某个观测指标(本例中是X1和X2前后两次观测),每个cell(格)中是每个学生的每次观测值(即上述公式中的x1i或x2i,在本例中取值1到7)。按ANOVA的术语,每个xi受到三个来源的影响:一是between-columns effects(在本例中是over-time effects,但内容分析的inter-coder reliability则是两个coders之间的coder effects、等等);二是within-columns effects(在本例中是within-subjects effects,即每个学生的特定因素);三、无法被columns和rows所解释的残差。三者之间,残差和within-columns effects 总是(假定为)random(随机)的,前者是ANOVA能够成立的必要前提、而后者则是因为n个学生是从N总体中随机抽取的一个样本。剩下的between-columns effects则需要根据研究设计、数据采集方式等各种因素而来确定是fixed(固定)还是随机的,因此而形成了你所提到的三种模型:
| Source of Variance | One-way Random Model ICC (1) | Two-way Random Model ICC (2) | Two-way Mixed Model ICC (3) |
| Within-columns effects | Random | Random | Random |
| Between-columns effects | – | Random | Fixed |
首先来看ICC(1)。它并不考虑X1和X2的区别,所以实际上是将数据表中的X1和X2两列数据合成一列(即图b的结构,其中共有2n行),为了说明图a和图b的相等性,我在图b中加了变量Time,但实际上ICC(1)模型是估算Time的,而是只含一个因子(即自变量)的one-way ANOVA(单因子方差分析)。其自变量是ID,当只有两个重测指标时,自变量的values(即unique的ID数)很多、但每个value下面只有2个cases(所以是个很奇怪的模型),其F值是用来检验每个学生的均值全部为零的假设。由此可见,ICC(1) 并不能检验X的重测信度(当然它有很多其它用途,尤其是作为一个基准模型)。你说看到“过去的文献,针对同一道问题,如上题,三种算法都被用过”。我很难想象这种情况。建议你搞清作者用ICC(1)检验的零假设到底是什么。
回到图a的常见数据。如上所说,它可以用来同时分解columns和rows的影响,也就是ICC(2) 和 ICC(3) 所需要的数据。所以ICC(1) 和 ICC(2) 都可以用来检验重测信度。两者的区别在于如何看待我开始时说的“同一概念的各种测量指标”的产生机制。这不是一个统计问题、而是研究设计问题或数据采集方法问题,即取决于每个研究的具体情况。一般而言,如果X1和X2是该概念的所有可能测量指标(最极端的例子是“匹配”样本,如夫妻、双胞胎、师生、上下级等“对子”对同一问题的回答),那么它们应该是fixed。反之,如果该概念除了Xk和X2之外,还可以有X3、… Xk指标,那么它们应该是random的。同理,检验在内容分析的inter-coder reliability时,coders应该都是从一个理论上无限大的总体中抽出来的样本,所以也应该是random的。你说你的两次测试是“two same judges in different time with fixed effect”,我没有足够信息来否定你,但直觉上感到它们是无限空间中的两个时间样本点,所以为什么不是random的?
我们还可以从模型结果的使用来理解between-columns effects到底是fixed还是random的。如果你只想(或只能)将其结果限制在本研究的具体时空中(如这两个特定测量时间点、这两个特定coders、等等),那么可以采用fixed模型(3);反之如果你希望将结果推及其它时间或空间(其它任何测量时点、任何coders、等等),那么就应该用random模型(2)。
除了between-columns effects的不同选择之外,ICC还涉及其它两个层面的选择,一是估算的ICC是consistency还是absolute agreement(两者的差别就是我上面提到的旧帖中描述的correlation与difference),二是single 还是average。这些分别涉及到一些新的问题,暂且不谈了。
如果谁真的要用ICC,应该认真读一下ICC的权威文献:K. O. McGraw & S. P. Wong (1996).Forming inferences about some intraclass correlation coefficients、以及该文的纠错补充。
最后,想说几句感受。常有网友在此问及各种进阶的统计问题、如SEM、multilevel、ICC等等。我是又喜又愁。喜的是后生可畏,敢于玩前沿。愁的是(从提问中推测),有关网友缺乏必要的基础知识,借助于统计软件而捷径上山、一步到顶峰。定量分析与其它绝大多数知识不同,只能循序渐进、一个台阶一个台阶往上爬。如果对进阶的方法不甚了了,与其大胆试用(大部分情况下会用错,而且错了还不知道原因何在),我强烈建议使用熟悉的经典方法,如回归、方差、crosstabs等等。经典方法也许用到你的数据上会有些问题、但那是已知的问题,而新方法可能带来的风险是无法预知。如果医生不了解某一新药,绝不敢乱用,而会使用已知作用有限并有副作用的旧药。我们是给数据看病的Data Doctor,也要有如此的基本医德。共勉。


