差异分析主要用于:(1)判断因变量在两组或多组之间的统计学差异,各组之间可以是独立的,也可以是非独立的;(2)如果多组之间存在差异,进一步开展两两比较,分析差异来源。
比如,分析不同医疗机构医生收入水平的差异。收入水平是因变量,医疗机构是自变量,自变量可以分为互相独立的3组:基层医院、二级医院和三级医院。再如,判断受试者在运动干预前后的心率是否存在差异。心率是因变量,自变量是时间,可分为干预前和干预后非独立的两组,示例如下:
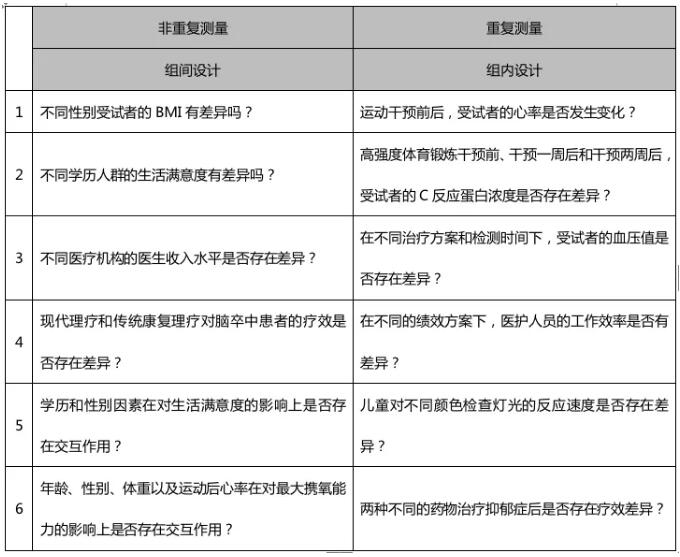
2、 判断研究设计类型
差异分析的研究设计类型主要分为三种:组间设计、组内设计和混合设计,具体如下:
2.1组间设计
组间设计是指研究中的各组相互独立,组别互斥,即研究对象只能存在于一组,不能分属于不同组别。
比如,研究不同性别受试者的BMI差异,BMI是因变量,性别是自变量,包含两个相互独立的组别:组1男性和组2女性。在该研究中,组1和组2是互斥的,即某一位受试者只能是男性(组1),或只能是女性(组2),不能既是男性又是女性。
再比如,研究酗酒者和非酗酒者的谷丙转氨酶差异,谷丙转氨酶是因变量,是否酗酒为自变量,包含两个相互独立的组别:组1酗酒和组2不酗酒。同样的道理,受试者只能是酗酒者(组1)或非酗酒者(组2),不能既是酗酒者又不是酗酒者,即组1和组2互斥,相互独立。
组间设计示例如下:
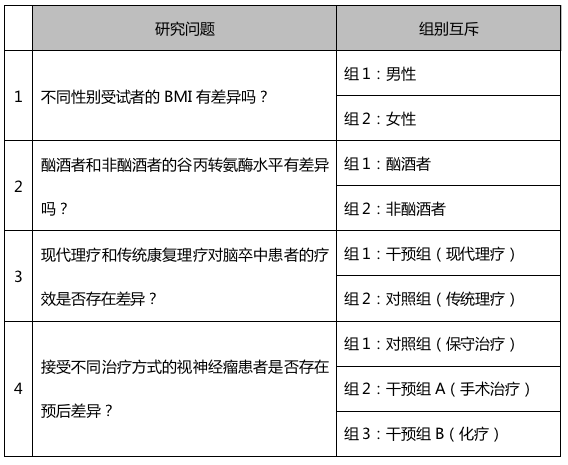
2.2组内设计
组内设计,又称重复测量设计,是指研究中的各组相互关联,所有研究对象均可分属于不同组别。简单来说,组内设计就是对研究对象进行重复多次测量,或对同一研究对象开展多种干预(常见于交叉设计)。
比如,分析运动前后,受试者心率的变化。心率是因变量,时间是自变量,包含两个相互关联的组别:时间点1(运动前)和时间点2(运动后)。在该研究中,时间点1和时间点2并不互斥,即运动后的研究对象与运动前一样,是同一群受试者接受了两次心率检测,任一位受试者既属于时间点1,又属于时间点2。如果我们针对同一群受试者增加重复测量次数,那么该研究仍是组内设计,研究类型不变。
再比如,研究绩效方案对医护人员工作效率的影响,工作效率是因变量,绩效方案是自变量,包含两个相互关联的组别:干预1(无绩效方案)和干预2(有绩效方案)。在该研究中,干预1和干预2也不互斥,是针对同一群医护人员分析有无绩效方案的差异,任一位受试者既属于干预1,又属于干预2。
此外,匹配设计也属于组内设计。比如上述例子中,如果有无绩效方案的医护人员并不是同一群人,但两组受试者在与工作效率相关的因素上存在匹配,我们就认为他们是一样的,符合组内设计的要求。但是在将匹配设计视为组内设计时我们需要十分谨慎,保证匹配后的研究对象一致。
组内设计示例如下:
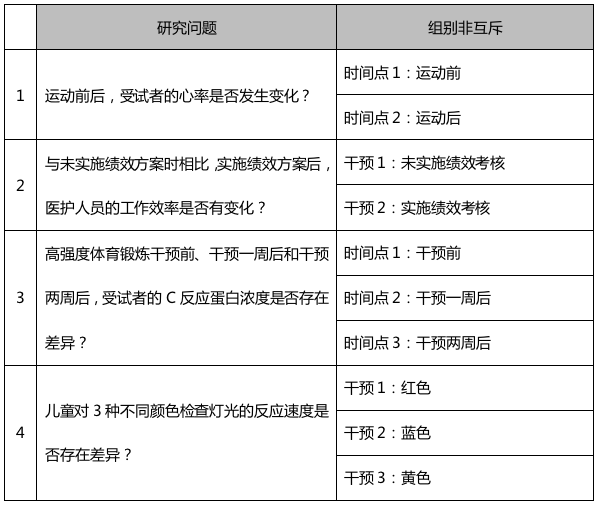
2.3混合设计
混合设计兼容了组间设计和组内设计的特点,至少包含1个组间因素和1个组内因素。比如,拟研究锻炼强度对C反应蛋白浓度的影响,将受试者随机分为对照、中强度体育锻炼干预和高强度体育锻炼干预三组,并在干预前、干预1周后和干预2周后重复测量3次所有受试者的C反应蛋白浓度。
在该研究中,C反应蛋白浓度是因变量,干预和时间是自变量。其中,干预是组间因素,各组别相互独立;时间是组内因素,各组别之间并不互斥,示例如下:
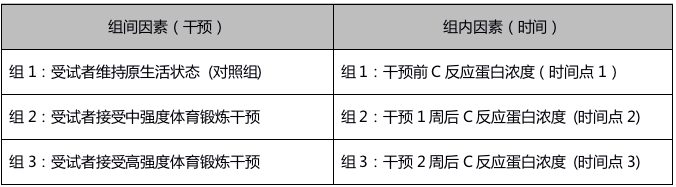
3、判断自变量数量
包含一个或多个自变量时,差异分析所采取的统计方法是不同的。那么,怎么判断自变量的数量呢?我们分别就包含一个自变量和多个自变量的研究进行了举例,帮助大家理解。
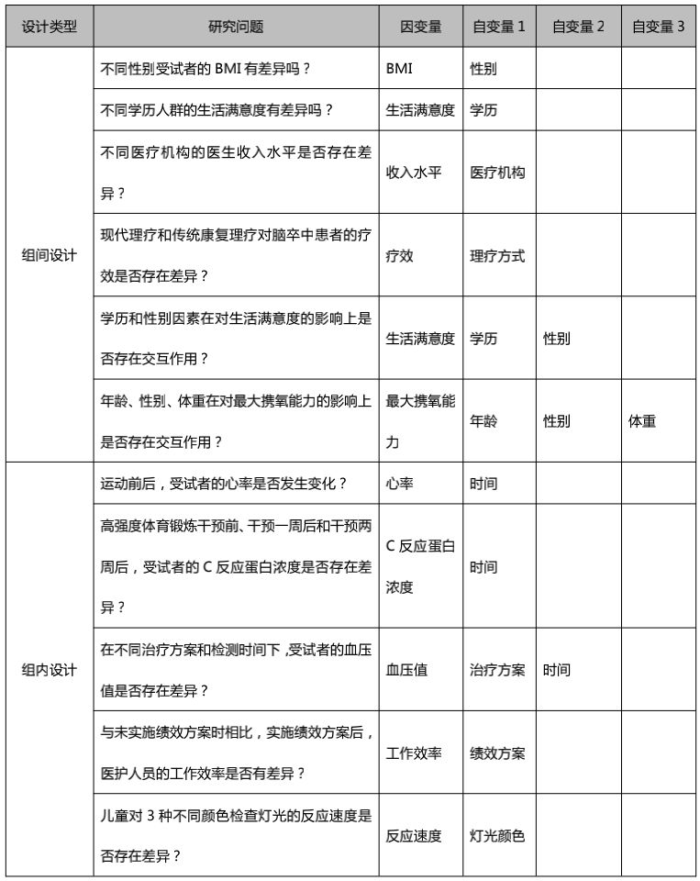
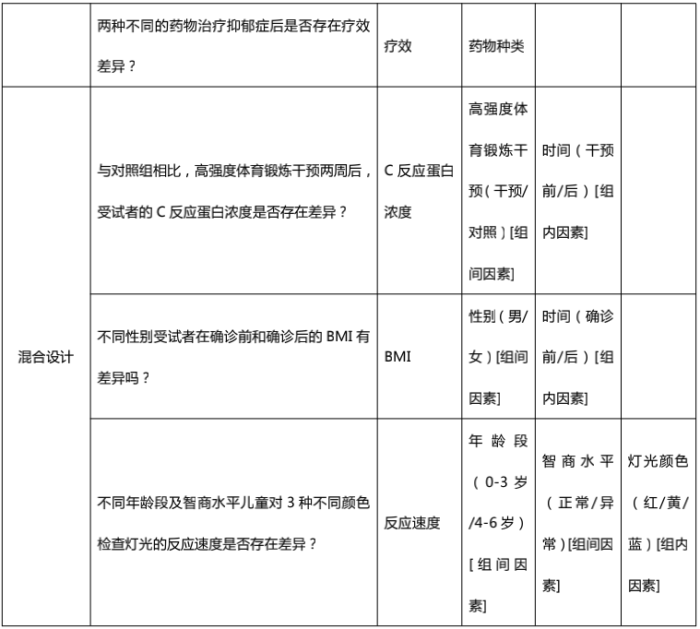
4、判断自变量组数
当只有一个自变量时,我们还需要进一步区分自变量的组数来选择合适的检验方法,一般分为2组或3组及以上,示例如下:
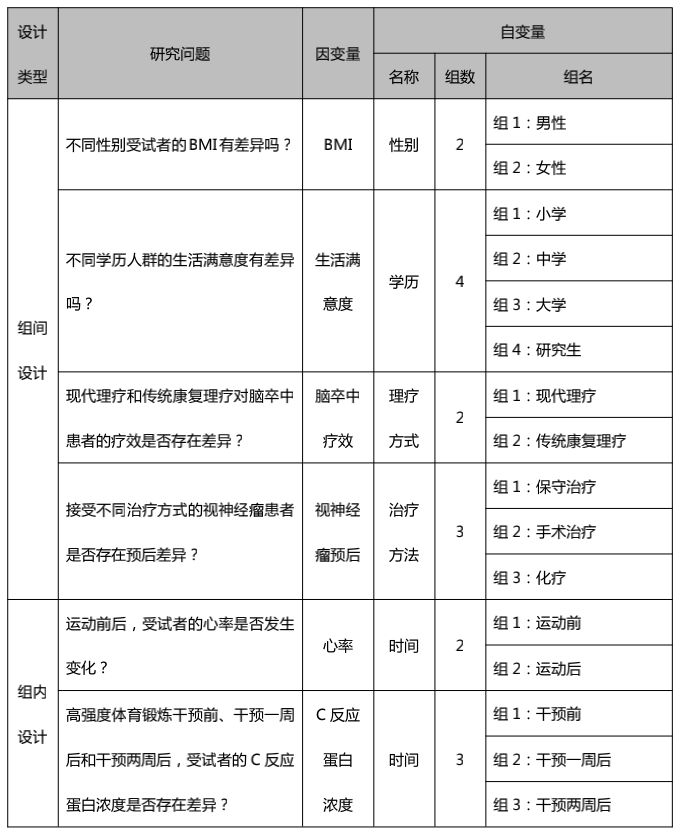
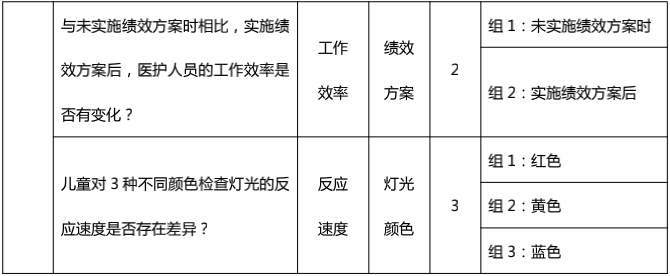
5、判断协变量
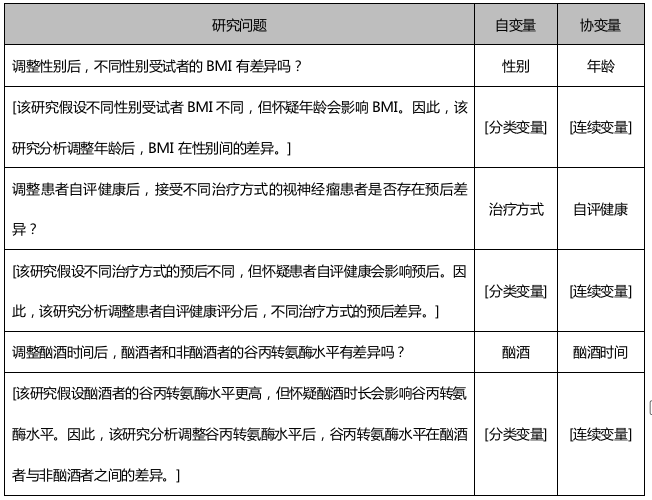
在差异分析中,如果关注因变量和一个分类型主要自变量之间的关系,同时需要考虑其它因素对其差异的影响,这就需要纳入协变量。纳入协变量是为了去除该类因素对主要观察变量差异的影响。调整该类因素后,可以减少其对研究结果的干扰,更加准确地分析两个主要观察变量之间的差异,保证结果的真实可靠性。示例如下:
6、判断因变量的数量
医学领域多关注一个因变量与一个或多个自变量之间的分析,很少联合多个因变量开展统计检验。但其实,很多研究同时包含多个连续型因变量。
比如,分析干预一段时间后酗酒者和非酗酒者的身体水平差异,往往会收集一系列健康相关指标,如谷丙转氨酶、血压、血糖、甘油三脂等。针对该研究,有2种统计分析方法:(1)分别对每一个因变量进行分析,开展多项统计检验;(2)联合多个因变量,在一项检验中分析所有数据。第1种方法是医学领域常用的处理方式,本文只介绍分别对每个因变量进行分析的情况。
7、检验方法选择
7.1组间设计
7.1.1只有一个自变量
7.1.1.1自变量有2组
(1)因变量为连续变量
独立样本t检验。该检验适用于分析连续型因变量在2个独立分组之间的均值差异。
(2)因变量为有序分类变量
Mann-Whitney U检验。该检验又称Wilcoxon-Mann-Whitney检验,适用于分析连续型或有序分类型因变量在2组之间差异的非参数检验方法。
(3)因变量为二分类变量
①卡方检验
比较二分类变量在2组之间的差异,实际上就是在分析比例差异。如果满足最小样本量的要求,可以通过卡方检验比较比例差异。
②相对风险(RR值)
相对风险是前瞻性队列研究或RCT中的常用指标,可以在一定条件下比较两个比例之间的关系,但其提示的结果是比值而不是差异。
③比值比(OR值)
比值比可以计算多类研究的差异,也是很多统计检验(如二分类logistic回归)的常用指标。在相对风险指标不适用的病例对照研究中,比值比仍可以很好地反映结果。
④Fisher精确检验
Fisher精确检验可以用于检验两个比例之间的统计学差异。
(4)因变量为无序分类变量
卡方检验。该检验常用于分析无序分类变量之间的关系,不区分自变量和因变量,因变量和自变量互换统计结果不变。
7.1.1.2自变量包含3个及以上组别
(1)因变量为连续变量
单因素方差分析。该检验适用于分析连续型因变量在2个或多个独立分组之间的均值差异。包含3个及以上组别时,可以开展两两比较分析差异来源。
(2)因变量为有序分类变量
Kruskal-Wallis H检验。该检验是非参数检验方法,适用于分析连续型或有序分类型因变量在2组或多组之间的差异。
(3)因变量为二分类变量或无序分类变量
卡方检验。该检验常用于分析无序分类变量之间的关系,也可以用于分析二分类变量(比例)在3个及以上组别之间的差异。如果存在差异,可以进行两两比较分析差异来源。
7.1.2包含2个及以上自变量
包含两个及以上自变量时,如果关注因变量和一个分类型主要自变量之间的关系,同时需要考虑另外1个因素对其差异的影响,可以使用单因素协方差分析。除此之外,一般采用回归分析的方法。


