本文介绍如何进行多个组比较(Fisher精确检验)及组间两两比较的卡方检验。
问题与数据
某医生拟探讨是否可以通过改善生活方式,如增强体育锻炼、减小体重及改善饮食习惯等,降低患者的胆固醇浓度。
现该医生招募了32例高胆固醇、生活习惯差的受试者,并将其分成3组。其中一组给予降胆固醇药物,一组给予饮食干预,另一组给予运动干预。经过6个月的试验后,该医生重新测量受试者的胆固醇浓度,分为高和正常两类。
该医生收集了受试者接受的干预方法(intervention)和试验结束时胆固醇的风险程度(risk_level)等变量信息,并按照分类汇总整理出频数(freq)变量,数据如下:
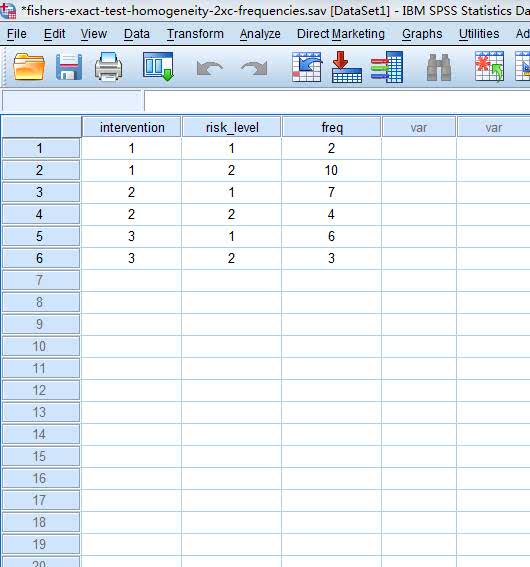
注:本研究将胆固醇浓度分为“高”和“正常”两类,只是为了分析方便,并不代表临床诊断结果
对问题的分析
为更好地介绍Fisher精确检验(2×C)分析方法,并说明其与卡方检验(2×C)的区别,本期仍使用卡方检验(2×C)的例子,但对数据模型进行了调整,使其更符合Fisher精确检验(2×C)的要求。
进行Fisher精确检验(2×C)也需要满足5项假设:
假设1:观测变量是二分类变量,如本研究中试验结束时胆固醇的风险程度变量是二分类变量。
假设2:存在多个分组(>2个),如本研究有3个不同的干预组。
假设3:具有相互独立的观测值,如本研究中各位受试者的信息都是独立的,不会相互干扰。
假设4:研究设计必须满足:
(a) 样本具有代表性,如本研究在高胆固醇、生活习惯差的人群中招募32例受试者;
(b) 目的分组,可以是前瞻性的,也可以是回顾性的,如本研究中将受试者分成3组,分别给予降胆固醇药物、饮食和运动干预。
假设5:样本量较小,即存在预测频数小于5的情况。
经分析,本研究数据符合假设1-4,那么应该如何检验假设5,并进行Fisher精确检验(2×C)呢?
思维导图
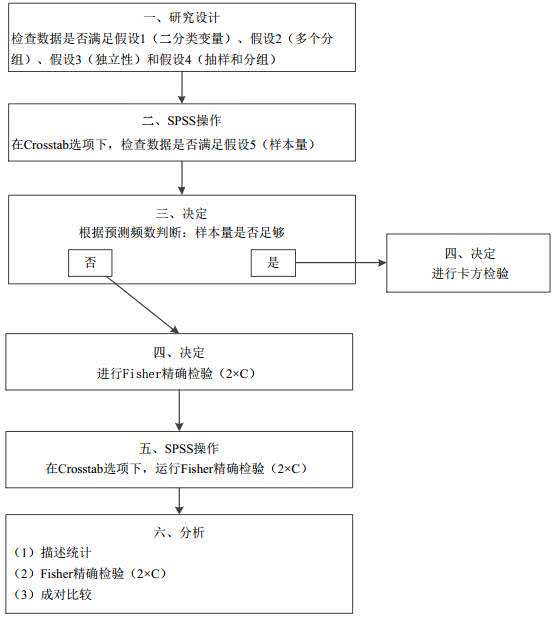
SPSS操作
4.1 数据加权(在使用整合数据的情况下)
在进行正式操作前,我们需要先对数据加权,如下:
(1) 在主页面点击Data→Weight Cases
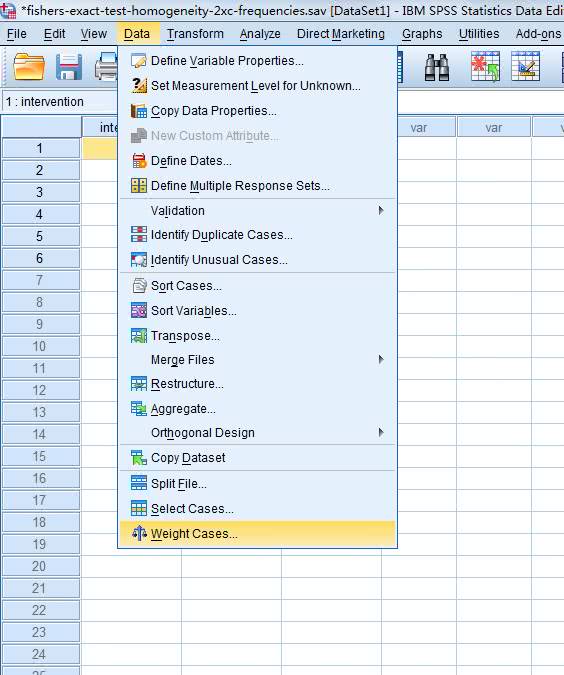
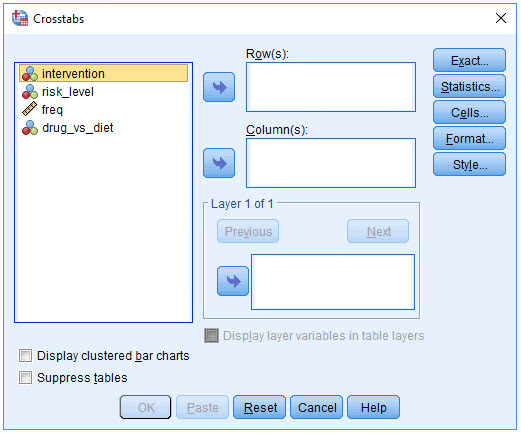
弹出下图
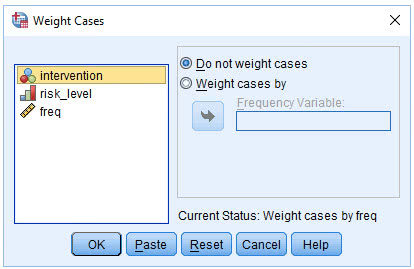
(2) 点击Weight cases by,激活Frequency Variable窗口
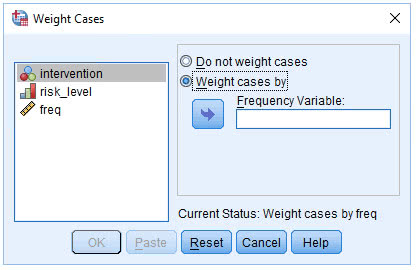
(3) 将freq变量放入Frequency Variable栏
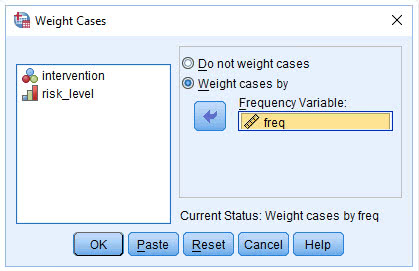
(4) 点击OK
4.2 检验假设5
数据加权后,要判断研究数据是否满足样本量要求,如下:
(1) 在主页面点击Analyze→Descriptive Statistics→Crosstabs
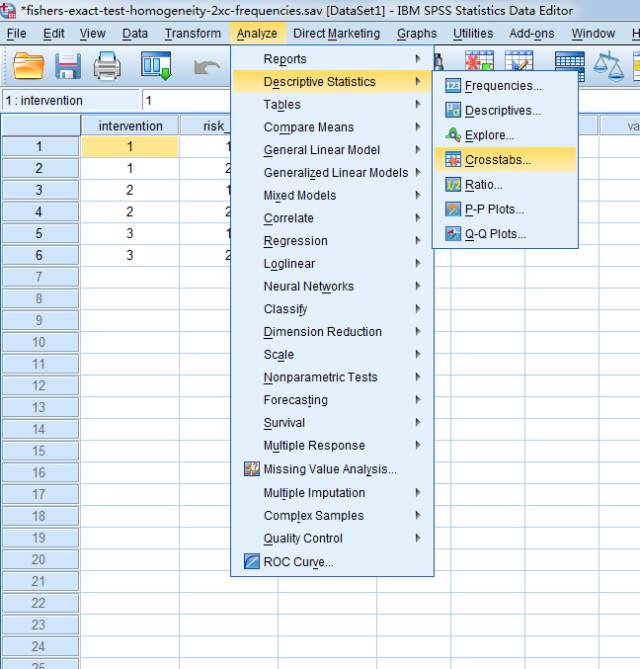
弹出下图
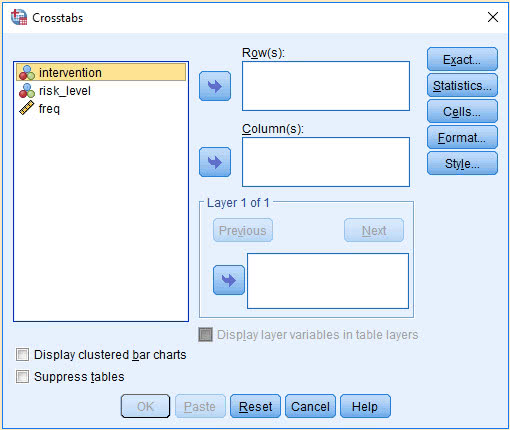
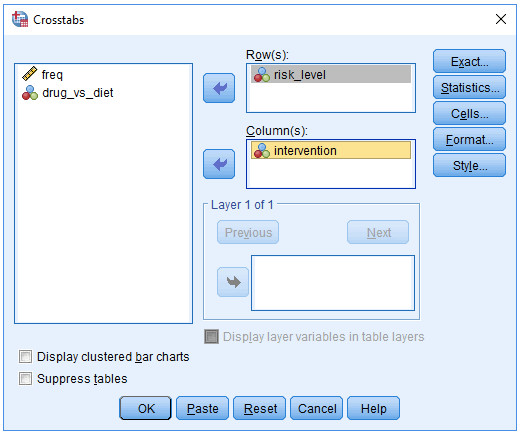
(2) 将变量risk_level和intervention分别放入Row(s)栏和Column(s)栏
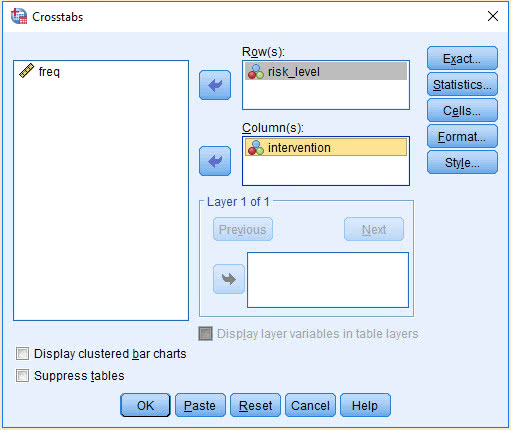
(3) 点击Statistics,弹出下图
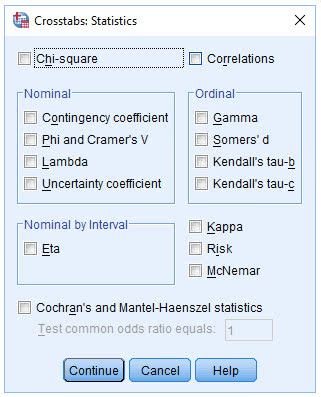
(4) 点击Chi-square
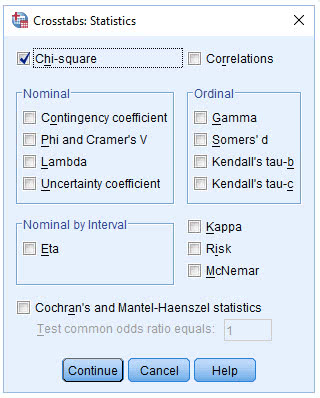
(5) 点击Continue→Cells
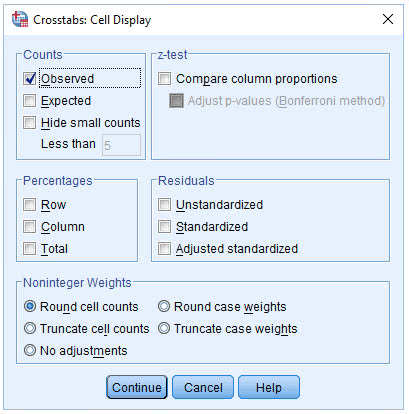
(6) 点击Counts栏中的Expected选项
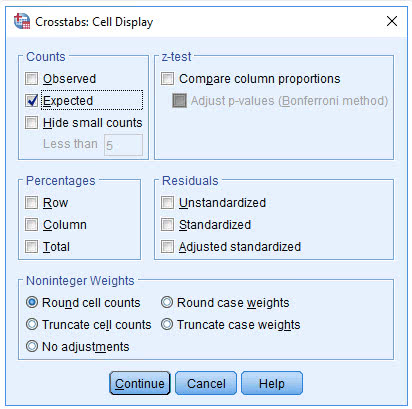
(7) 点击Continue→OK
经上述操作,SPSS输出预期频数结果如下:
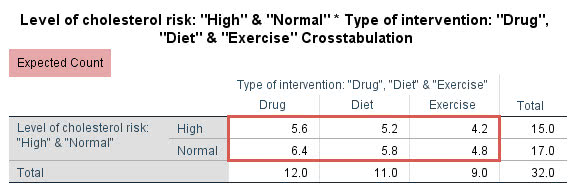
该表显示,本研究最小的预测频数是4.2,小于5,满足假设5。
Chi-Square Tests表格也对该结果做出提示,如下标注部分:
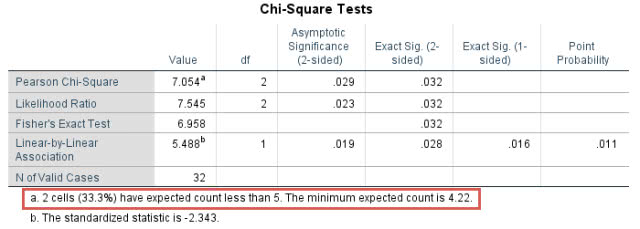
即在本研究中,存在小于5的预测频数,无法进行卡方检验(2×C),需进行Fisher精确检验(2×C)。
4.3 Fisher精确检验(2×C)的SPSS操作
(1) 在主页面点击Analyze→Descriptive Statistics→Crosstabs

弹出下图

(2) 点击Exact,弹出下图
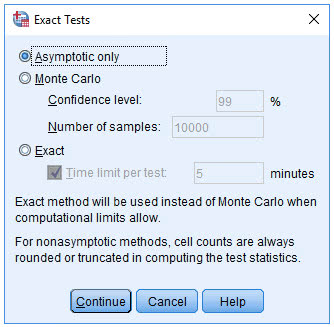
(3) 点击Exact栏,激活Time limit per test,并填写数字“5”
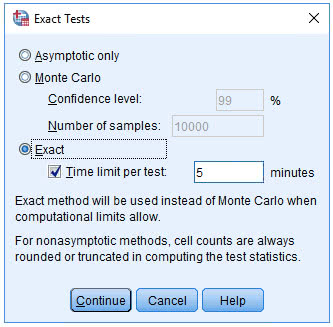
(4) 点击Continue→Statistics,弹出下图

(5) 点击Chi-square

(6) 点击Continue→Cells

(7) 点击Percentage栏中的Column选项
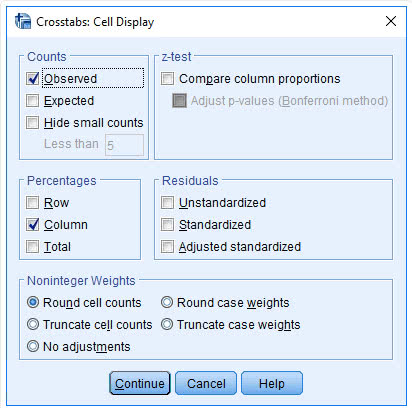
(8) 点击Continue→OK
4.4 组间比较
Fisher精确检验(2×C)需要逐对筛选变量,再进行比较。我们仅以药物和饮食干预两组的组间比较为例,SPSS操作如下:
选择变量
(1) 在主页面点击Data→Select Cases
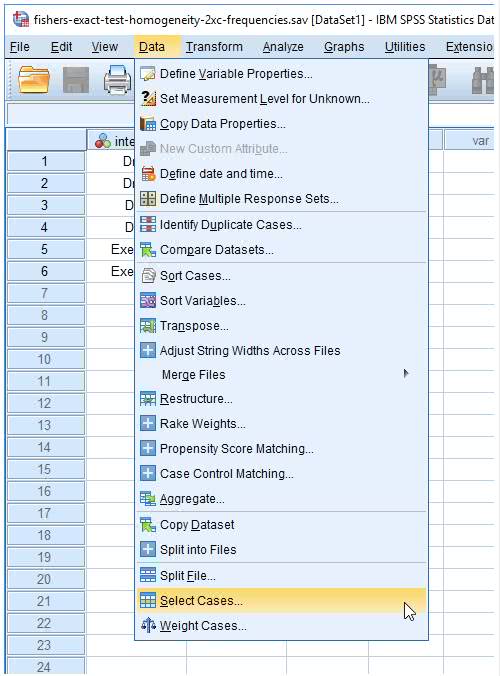
弹出下图
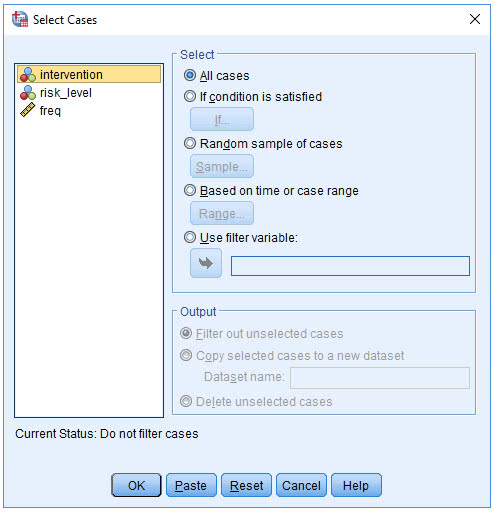
(2) 在Select栏中点击If condition is satisfied
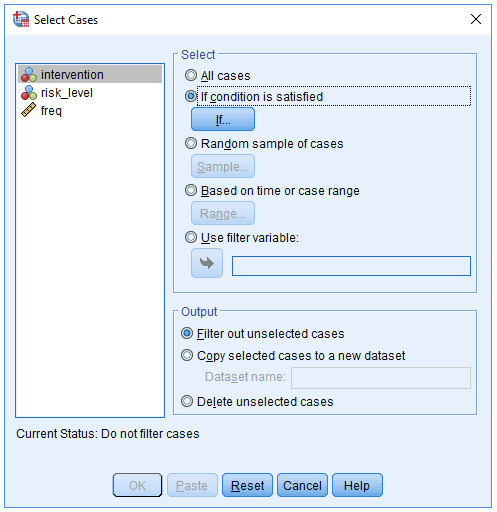
(3) 点击if,弹出下图
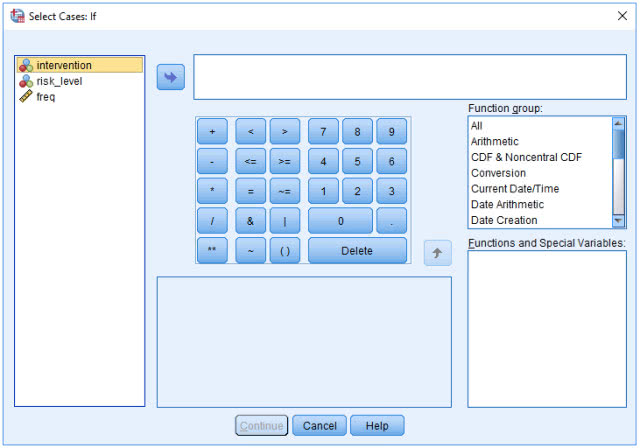
(4) 在右上栏中输入“intervention = 1 | intervention = 2”
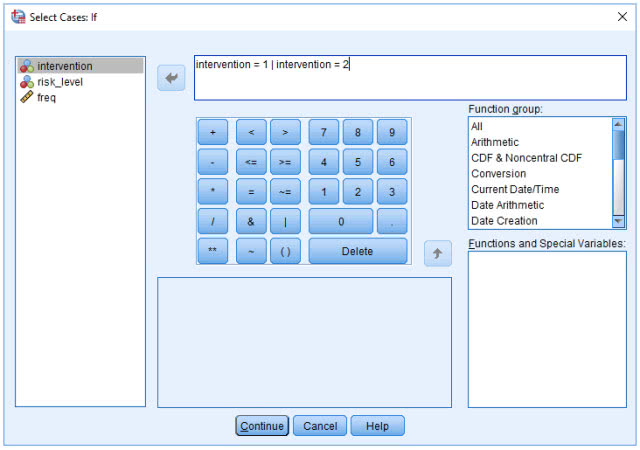
(5) 点击Continue→OK,弹出下图
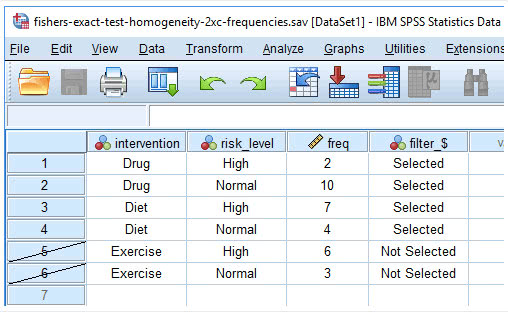
两两比较
(1) 在主页面点击Analyze→Descriptive Statistics→Crosstabs
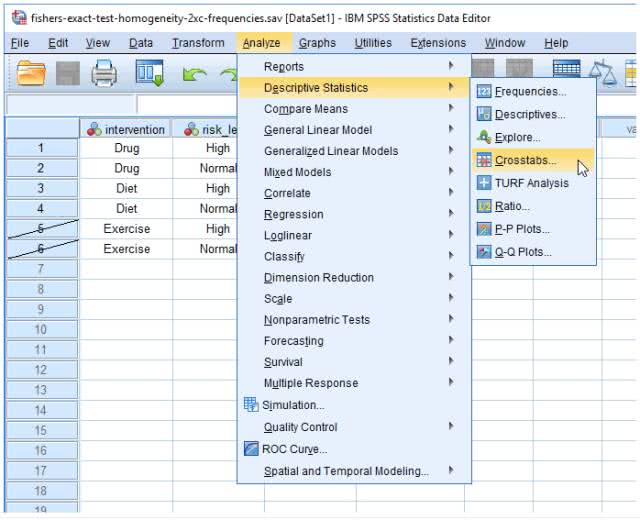
弹出下图
(2) 将变量risk_level和intervention分别放入Row(s)栏和Column(s)栏
(3) 点击Exact,弹出下图
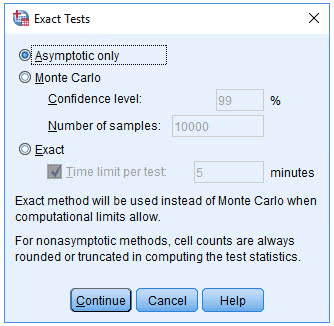
(4) 点击Exact栏,激活Time limit per test,并填写数字“5”
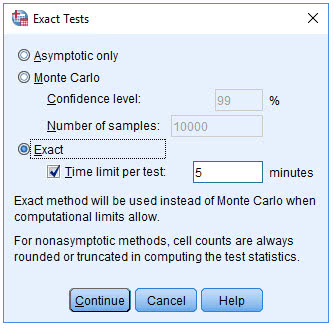
(5) 点击Continue→Statistics
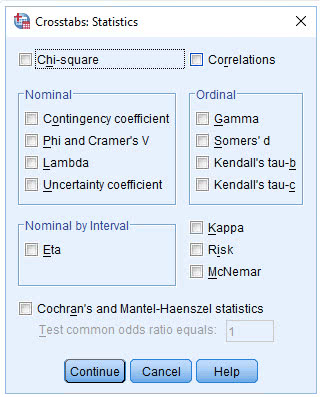
(6) 点击Chi-square
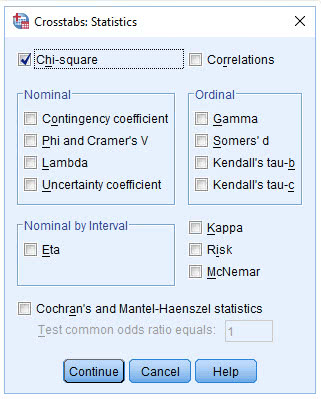
(7) 点击Continue→Cells
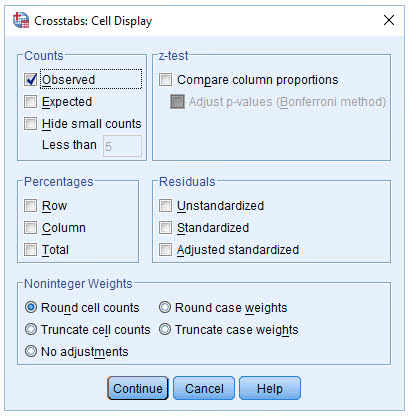
(8) 点击Percentage栏中的Column选项
(9) 点击Continue→OK
结果解释
5.1 统计描述
在进行Fisher精确检验(2×C)的结果分析之前,我们需要先对研究数据有个基本的了解。SPSS输出结果如下:
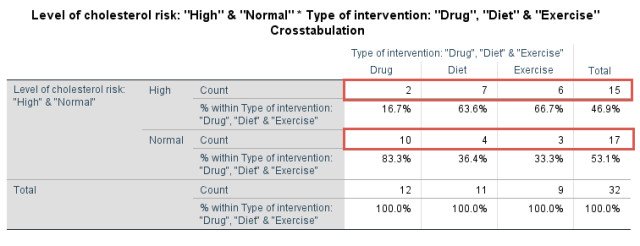
该表提示,本研究共有32例受试者,根据干预方式均分为3组。在试验结束时,药物干预组的12例受试者中有2例胆固醇浓度高,饮食干预组的11例受试者中有7例胆固醇浓度高,而运动干预组的9例受试者中有6例胆固醇浓度高。
由此可见,药物干预比饮食或运动干预的疗效更好。同时,该表也提示,药物干预组的12例受试者中有10例胆固醇浓度下降,饮食干预组的11例受试者中有4例胆固醇浓度下降,而运动干预组的9例受试者中只有3例胆固醇浓度下降,如下标注部分:
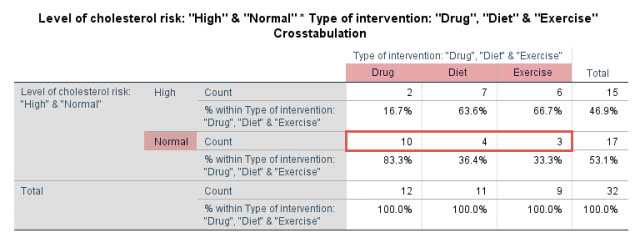
但由于各组样本量不同,频数会误导人们对数据的理解。因此,我们推荐使用频率来分析结果,如下标注部分:
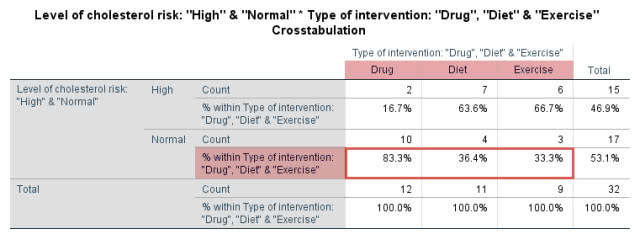
该表提示,药物干预组的12例受试者中83.3%胆固醇浓度下降,饮食干预组的11例受试者中36.4%胆固醇浓度下降,而运动干预组的9例受试者中只有33.3%胆固醇浓度下降,提示药物干预比饮食和运动干预更有效。但是这种直接的数据比较可能受到抽样误差的影响,可信性不强,还需要进行统计学检验。
5.2 Fisher精确检验(2×C)结果
本研究中存在预测频数小于5的情况,根据Chi-Square Tests表格分析各组的差别。SPSS输出检验结果如下:
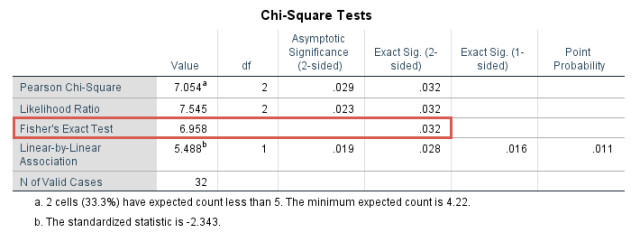
Fisher精确检验结果显示P= 0.032,小于0.05,说明本研究中各组之间率的差值与0的差异具有统计学意义,提示药物干预与饮食、运动干预在降低受试者胆固醇浓度的作用上存在不同。如果P>0.05,就说明各组之间的差值与0的差异无统计学意义,即不认为各组之间存在差异。
5.3 Fisher精确检验(2×C)中的成对比较分析
Fisher精确检验(2×C)的结果是比较模糊的,只能判断各组之间是否存在差异,但不能说明是哪两组之间存在差异。因此,我们需要对Fisher精确检验(2×C)的各组进行成对比较分析。但是,成对比较会增加出现I型错误的风险。我们需要根据Bonferroni调整后的α水平判断成对比较的统计显著性。
一般来说,调整α水平是原α水平与分组数量的比值,如下表:
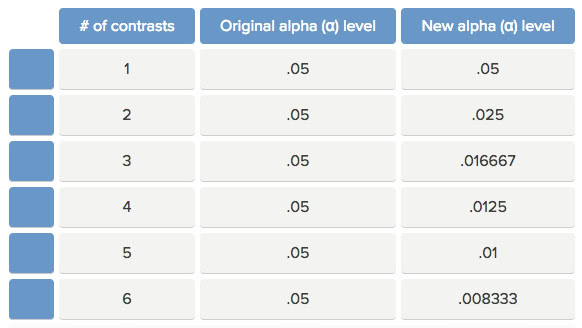
针对本研究来说,调整α水平为0.016667,即原α水平(0.05)与分组数量(3)的比值。如果成对比较的P值小于0.016667,就说明两组之间的差异具有统计学意义;但如果成对比较的P值大于0.016667,就说明两组之间差异无统计学意义。
SPSS输出药物和饮食干预两组的组间比较结果如下:
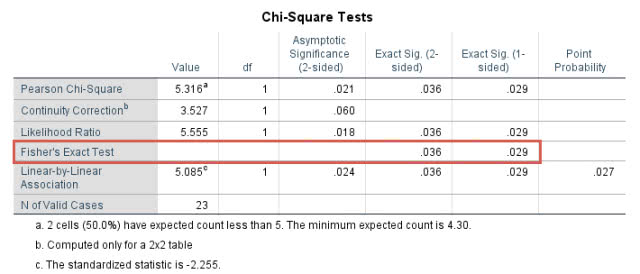
该表提示药物干预的降胆固醇作用与饮食干预的降胆固醇作用的差异无统计学意义(P=0.036,大于0.016667)。
同样地,SPSS输出药物和锻炼干预两组的组间比较结果如下:
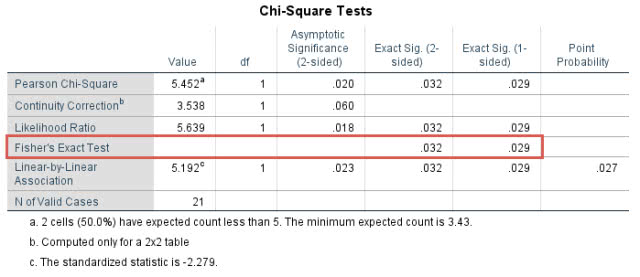
该表提示药物与锻炼干预降胆固醇作用的差异也无统计学意义(P=0.032,大于0.016667)。
SPSS输饮食和锻炼干预两组的组间比较结果如下:
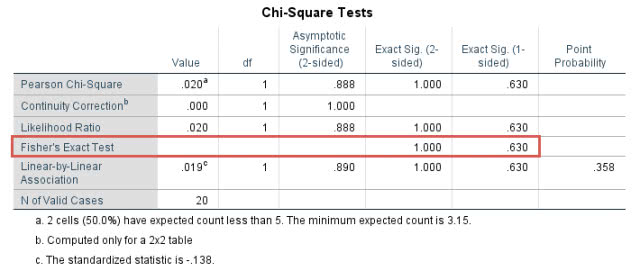
该表提示饮食与锻炼干预降胆固醇作用的差异也无统计学意义(P=1.000,大于0.016667)。
综上可见,本研究中药物、饮食与锻炼3组干预的降胆固醇作用,成对比较均无差异。即使Fisher精确检验(2×C)的P值小于0.05,也可能出现各组之间成对比较结果无差异的情况。
采用Bonferroni调整后的α水平进行判断,结果比较保守。如果仍使用0.05为α水平,就会提示药物干预与饮食、运动干预的降胆固醇作用的差异存在统计学意义(P<0.05)
撰写结论
本研究招募32例高胆固醇、生活习惯差的受试者,分别给予药物、饮食和运动干预。试验结束时,药物干预组12例受试者中有10例(83.3%)胆固醇浓度下降,饮食干预组11例受试者中有4例(36.4%)胆固醇浓度下降,而运动干预组9例受试者中有3例(33.3%)胆固醇浓度下降。
Fisher精确检验(2×C)结果显示,3组差异具有统计学意义(P=0.032)。采用Bonferroni调整后显示,药物、饮食与锻炼3组干预的降胆固醇作用,成对比较差异无统计学意义(P>0.016667)。


