以正态分布均数的可信区间计算为例。传统的计算方法是需要知道样本的均数、标准差、样本含量,通过以下公式进行计算:
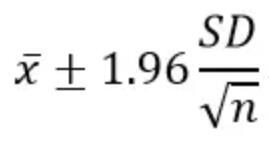
Bootstrap法也叫靴襻法,在SPSS 17.0版本开始出现,其基本思想是:某个统计量的所有准确度估计指标都来源于该统计量的抽样分布。如果这个统计量是用来源于某一个总体的含量为n的随机样本估计而得到的,那么它的抽样分布就可以显示该统计量的各种值的相对频数。抽样分布是由总体分布和估计统计量所用的计算公式所决定的。简而言之,其基本思想是通过对一个样本的重复多次放回抽样来估计总体的各种分布参数。
Bootstrap过程是:首先有一个实际观测到的数据集(称之为原始数据集),它含有N个观测,然后根据分析的需要确定计算某个统计量的公式。从这个数据集中有放回地随机抽取n个观测组成一个样本,称之为Bootstrap样本。在这个随机抽样中,原始数据集中的观测有的只被抽到1次,有的超过1次,也有的没有被抽到。利用这个被抽到的样本,按照事先确定的公式,计算出所需要的统计量。如此反复抽样和估计,最后由估计出的统计量的值组成一个数据集,利用这个数据集来反映该统计量的抽样分布。如果它的抽样分布是正态分布,利用标准差的计算公式可以估计该统计量的标准误及其95%可信区间;如果该抽样分布不是正态,可以用第2.5百分位数和第97.5百分位数来估计95%的可信区间。 那么我们在SPSS中如何利用bootstrap法估计可信区间呢?下面分别用均数和中位数为例子进行计算95%可信区间。 假设我们有一组病人(n=412)的年龄数据,需要估计这些病人年龄的均数的95%可信区间。只需要点选分析→描述统计→探索,把年龄变量放入“因变量列表”,点击统计量按钮,选择描述性(此处默认会计算均值的95%可信区间),同时点选Bootstrap按钮,点选“执行bootstrap”就可以了。
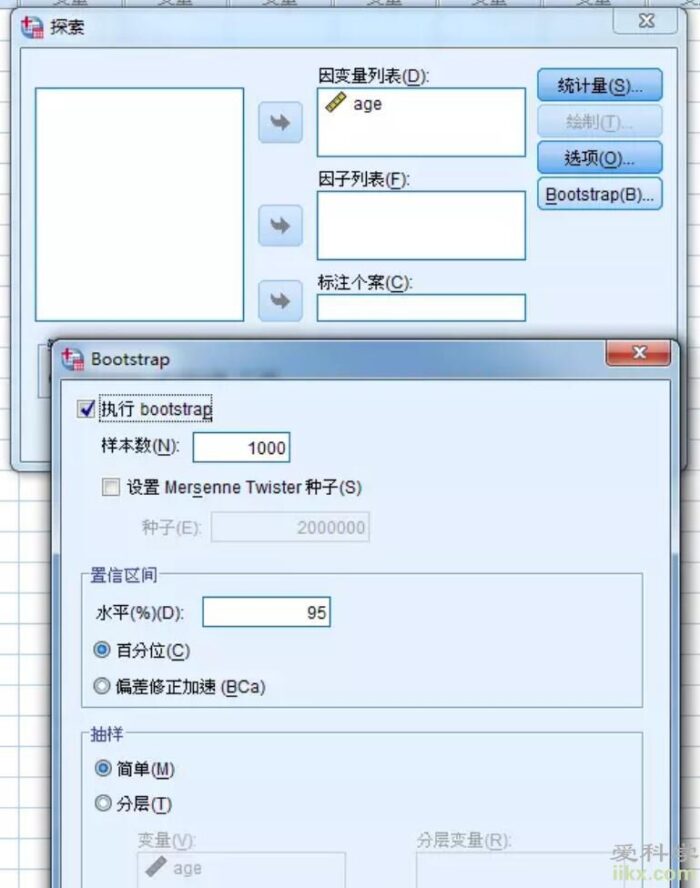
这时返回的结果如下:
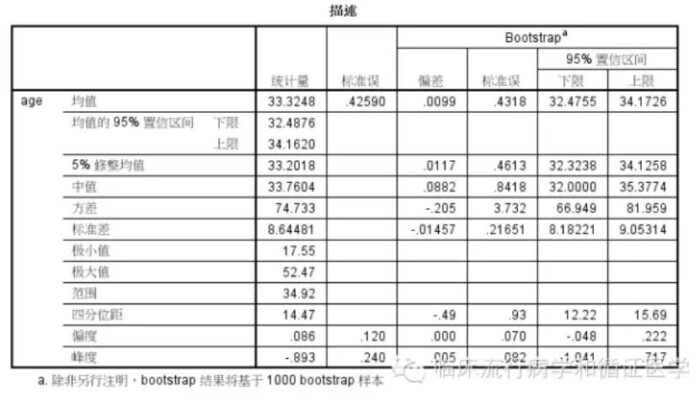
可见在SPSS通过传统方法计算得到的均数是33.3248,均数的95%CI是(32.4876,34.1620)而bootstrap法计算得到均数的95%CI是(32.4755,34.1726);两者计算的结果基本相等。此外,大家还可以看到中位数是33.7604,bootstrap法计算得到的中位数95%CI是(32.0000,35.3774)。 由于中位数95%可信区间的计算比较复杂,因此,使用Bootstrap法进行中位数可信区间的计算是一个比较好的方法。从上图可以看出,除了均数、中位数,其它统计参数的95%可信区间均可以通过Bootstrap法得到。 因此,当我们收集到的样本数据能很好的代表总体的时候,bootstrap法是一个很好的估计可信区间的方法。尤其是当某些指标的可信区间没有明确的公式可供使用的情况下,bootstrap法计算可信区间更是一个方便的计算方法。
参考文献: 刘勤金丕焕. Bootstrap方法及其在医学统计中的应用. 中华预防医学杂志. 1998. 32(1)


