一个回归分析模型美不美,关键点之一是我们如何对待连续型自变量。这里面有一些技巧,是大家需要重视的。
连续型自变量,首先要要明确,与研究结局Y是否具有线性关系。关于线性关系,无论是线性回归、logistic回归和Cox回归,都要明确自变量与结局存在着大致的线性关系。有些时候线性条件成立、有些时候线性条件不成立。现在我根据实际情况,介绍处理连续型自变量的若干种方法。
连续型自变量纳入回归模型的n种方法:
1 分析案例.
例3:研究究高血压患者血压与性别、年龄、身高、体重、户籍等变量的关系,随机测量了32名40岁以上的血压y、年龄X1、体重指数X2、性别X3,户籍X4试建立多重线性回归方程。
本例中年龄和体重指数是连续型变量,本文针对年龄开展分析。对于年龄与高血压的关系,有以下几种方法可以推荐给大家。
2 当自变量与应变量线性关系成立.
第一种,当线性关系条件成立,最基本的方法是直接纳入。直接纳入法是最原始的方法,当然线性关系成立,不用担心这样直接纳入是否合适。本例显示,年龄每增加一岁,血压增加1.697 mmHg。

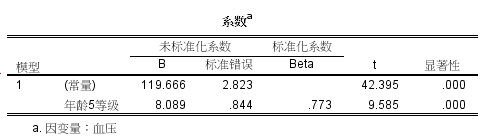
第二种,线性关系成立时,等级变量法。当线性关系条件成立,很多时候直接纳入自变量的方法,得到的回归系数,意义不大。比如,年龄每增加一岁,血压增加1.697 mmHg。没有太大的临床意义。如果我们现将年龄进行进行转换,变成有序多分类变量,也是不错的办法。比如,由于年龄在41-65岁之间,我把年龄变为41-45岁,46-50岁,51-55岁,56-60岁,61-65岁一组,然后再开展分析。我们就可以发现,结果解释的大致相同。本例显示,年龄每增加5岁,血压增加8.089 mmHg。这样的说法在临床上更有意义。
本方法有另外一种说法,叫做趋势性检验分析。
本方法需要注意等级变量等距的问题,若不等距,可能会得到错误的结果。
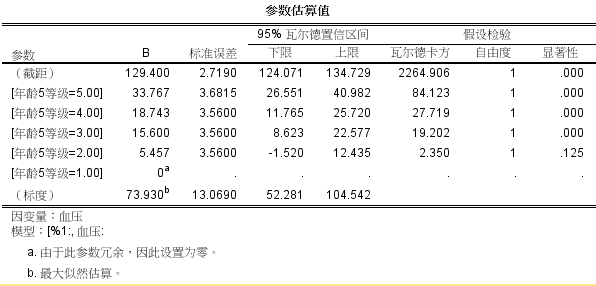
第三种,线性关系成立时,哑变量设置的方法。这种方法即在第二种方法的基础上进行哑变量设置分析,比如我们以41-45岁作为对照,开展哑变量分析。可以发现,哑变量设置的方法为我们提供了更多关于变量影响的信息。比如研究可以发现,实际上,不是所有的组别都和41-45岁相比,血压都增高的,45-50岁组与41-45岁相比,没有发现统计学差异(P=0.125)。
这种方法也有风险,它需要更大的样本量,它可能会由于各组别样本量不足而导致无统计学差异的结果。很多人会奇怪,比如下面的结果:
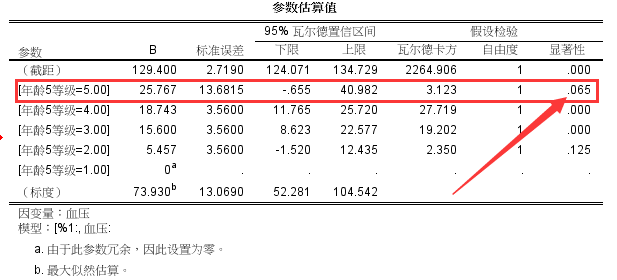
诸位可以看到,年龄处于第5等级时,b=25.767,是一个较大值,但是p=0.065, 没有统计学意义。虽然看起来随着年龄增加,血压是在不断上升,但是由于年龄处于第5等级时,样本量过小,抽样误差过大(标准误差=13.68),远远大于其他组别,因此P值也变得很奇怪。碰到这种情况,我还是推荐不设置哑变量的处理方法。
第四种,线性关系成立时,双重法。同时开展第三种方法(哑变量设置)和第二种方法(趋势检验法)。两者结合,珠联璧合!同时能够体现各亚组的效应,也可以体现总体上的线性关系。强烈推荐!
3 当自变量与应变量线性关系不成立.
当线性关系不成立,也有以下若干种方法。
第一种方法,当然线性条件不成立,哑变量设置方法。哑变量设置的方法是非常基础的方法。我们首先将定量自变量转为等级自变量,然后设置哑变量开展分析。
第二种方法,哑变量设置 趋势性检验方法。该方法同线性条件成立的第四种方法。很多人觉得奇怪,线性关系不成立,你怎么还用趋势性检验呀?其实很多时候我们在报告结果的时候,读者不知道到底线性条件是否成立,若我们同时展示哑变量设置的分析结果(部分哑变量有统计学效应)和趋势性检验结果(一般是阴性结果),那么我们便可以一方面详细报告我们的结果,而另一方面也告诉读者,自变量与结局线性关系不成立的, 因为趋势性检验结果不成立。
第三种方法,数据转换的方法。一般将连续型自变量通过x^2转换,或者log转换,或者e^x转换等多种形式建立与y的关系。
下文的关于线性条件的例子来自于《中华流行病学杂志》2019年第8期的文章:冯国双.观察性研究中的logistic回归分析思路[J].中华流行病学杂志,2019,40(8):1006-1009
举例: 某研究分析老年人高血压(二分类变量,是或否)的危险因素,研究因素包括gender、age、ox-LDL、Adiponectin、ox-LDL IgG和ox-LDL IgM共6个指标。其中gender为二分类变量,其余变量均为连续变量。如果把6个自变量直接纳入统计软件分析,所得结果见表 1。
表 1 统计软件直接给出的高血压影响因素分析结果
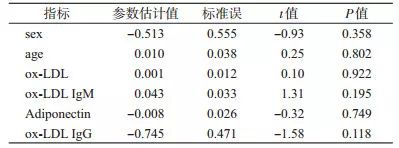
可以看出,6个变量均差异无统计学意义。然而对数据重新分析后发现,并不是这些变量对结局均无影响,只是未能发现它们之间的真实关系而已。经仔细观察,发现age和ox-LDL IgM对结局的影响是有统计学意义的,但不是线性影响,而是二次项关系(表 2)。
表 2高血压影响因素重新分析后的结果
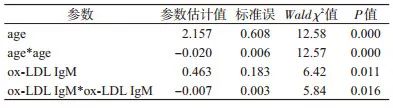
第四种方法,曲线回归的方法。曲线回归,经典的方法有两种,一种是LOESS回归,一种是限制性立方条样回归。这两种方法的共同特点是,绘制得到的统计图真是好看呀。
之前报道过LOESS回归:
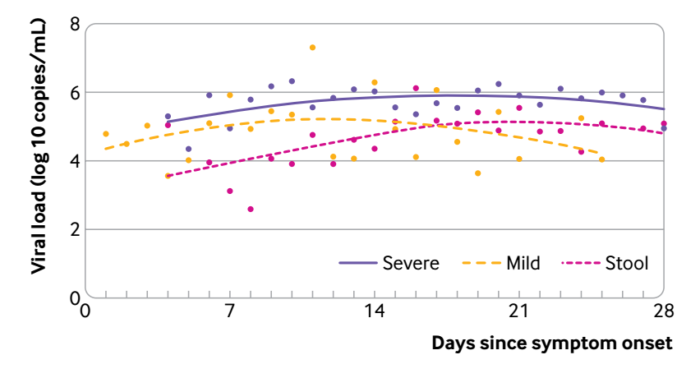
而限制性立方条样图,结果也非常不错。下面这张图利用logistic回归计算OR值的立方条样图,怎么样,不错吧?
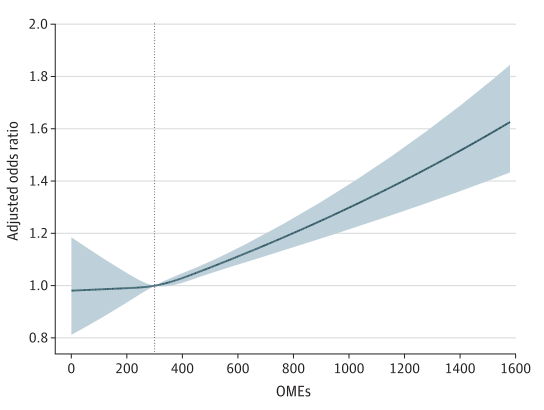
这两种非线性关系图,有点复杂,请有兴趣的同学们网上搜索研究,非常有意义哦。
第五种方法,各种方法大集合。如果遇到连续型自变量十分关键,我觉得可以多个角度去分析。哑变量设置、趋势性分析、限制性立方条样图结合一起玩一把,放在结果吧,那是非常酷的结果。
好了,关于连续型自变量,我就讲到这里。对于连续型自变量的处理,一定要打开思路,特别是如果这个自变量非常关键,诸位应考虑多种策略的组合。


