统计学是通过搜索、整理、分析、描述数据等手段,以达到推断所测对象的本质,甚至预测对象未来的一门综合性科学。
嗯,以上是统计学课本中对统计学的定义!
但是近日,一位来自谷歌的统计学家却发长文表示“统计学很无聊。“
这位统计学家叫 Cassie Kozyrkov,目前是 Google 的首席决策师。在这篇文章中,她提到:“别看我们平时都是在做一些看起来 ' 高大上 ' 的计算,其实核心都很单调的;另外,数据是很无聊的,人性化的事情才是难点。”
让我们先普及一些统计学的入门级概念,然后跟着这位统计学家一起,看看她的逻辑证明。

总体
当一个普通人想到“population”这个词时,他会想到什么?人,对吗?不只是一两个,而是很多,几乎是所有的人!在我们的学科中,它更像是所有的事物的集合。总体可以是人、像素、南瓜、神奇宝贝,或者任何你喜欢的东西。
总体是我们感兴趣的所有项目的集合。
先停一下,在总体的确定上是需要花点时间的,因为这是研究的基础。
规则是这样的:通过写下你对总体的描述,你就确定了你的总体是什么,除此之外没有任何东西可以影响你的决定。通过进一步阅读,你就能接受这些术语和相应的限定条件了。
提出你感兴趣的总体并没有听起来那么令人望而生畏,请记住,是由你自己来选择你想要感兴趣的事物。没有错误的选择,只要它是具体和全面的就可以是一个总体。接下来我会讲得很详尽,并且建议以下图中的树木作为本文感兴趣的总体。

如果我的总体是这片森林中的树木,那么它们就代表了我所关心的关于这个决定的一切。我对这些树感到很兴奋。坦白地说,这种兴奋是绝对真实的: 我非常喜欢这个图形,因为我在自己的讲座中使用它很多年了。请允许我再怀念它一次……当然,飞机上漂浮着一些树木,从空间上来说是非常合理的。
由于这是我的总体,我应该记住,我并没有理由从自己的分析中得出我已经从其他森林中的树木了解到的结论。我的发现充其量只适用于这些树木。最糟糕的是,嗯...... 我只想说数据科学家的生活中有时候是需要去构建特征的,不只是描述表面特征。
这里有你看不到的树吗?这样的研究没意义。它不是我们总体的一部分。挑选任何一棵树?同样没有意义,因为这不是你的整个总体。只有他们同时在一起对我们来说才是有意义的。这就是总体的概念。
样本
来自总体中的任意项目集合的样本。
样本是你拥有的数据,而总体是你“希望”拥有的数据。
这些橙色树木集合中的任何一个都是样本。我希望你们能有一些直觉知道哪个更好。在之后的文章中,我将告诉你如何使样本成为一个好样本。我将用这个例子的其余部分刺激专业人士来证明这一点。
观测值
观测值是对样品中单个项目的测量。
我们在这个蓝色标记的树上进行的测量是一个观测值。坚持使用精确语言的人会注意到,“sample”是一组观察结果的集合名词。从理论上讲,“samples”作为复数并不表示“观测到的多个值”,而是表示“多个观测值的集合”。
统计数据
啊哈!统计数据!这当然是很重要的,因为我们在研究了这些数据之后命名了我们的学科!
统计数据是通过任意一种方法去获得样本数据。
那么什么是统计数据?这只是统计我们拥有的数据的一种方式。是不是很失望,不用失望,事实证明,统计和统计学科是两码事。

统计数据的示例:如果我们对树的高度感兴趣,那么看到所有这些橙色标记树的平均高度等统计数据就不会感到惊讶。如果你愿意,你也可以采用那些样本树高,找到最高的前三个,把它们加起来,取对数,加上最低的两个树高的差值的平方根,通过这样的计算加工可以产生另一个统计数据!也许有用,也许不是那么有用,但也是一个统计数据。
如何证明统计学是无聊的
假设我们对树的平均高度感兴趣,对于这个样本,树的平均高度恰好是 22.5 米。这个数字对我们意义吗?
让我们回顾一下总体的概念:只对总体的研究是感兴趣的。这个样本是总体吗?不是。因此,它对我们来说并不重要。我们从一些无聊的树上取了一些无聊的测量值,然后我们把这些无聊的测量值进行加工计算……从这个过程中得出的结果也很无聊。
所以,我已经向你们证明了你们心中一直知道的事实:统计学是无聊的!证明完毕。
用词不当!
统计学家们疯了吗?为什么我们要用一些无聊的数字来命名我们的学科呢?实际上,这是用词不当。
如今我们对这些术语进行深度剖析,分析的是关于计算统计数据的学科,但统计学不仅仅是研究那些数据,而是要从那些数据中挖掘信息,从而实现对未知领域的探索,但也有可能这只是伊卡洛斯式的飞跃,最后得不到任何成果。
我们学科的真实名称(这个名称更能体现学科的含义)更加晦涩:统计数据的消化……但这听起来有点恶心,所以我们把它简化为平易近人的说法。
让我来解释一下。
参数
接下来讲我们的主角:参数。这个东西太花哨太闪亮。是那种演出结束后会获得一个花束的角色,它甚至有属于自己的希腊字母(通常是θ)。你可以将参数看作是总体里的一个统计量,它是由所有我们感兴趣的总体计算得来的,但是通常无法直接获得。
参数总结了总体特征
我们承认这些树木使我们深感兴奋,现在要我总结一下你关心的一切。

参数值显示:所有树木的真实平均高度恰好是 21.1 米。
想象一下,这是周六早上,你站在这片森林的空地中间。你还没测量过任何树木,但你超想知道这个数字,这是你梦寐以求的一切。
知道参数需要什么?
你必须精确的测量所有树!一旦做完了,你会有任何不确定的吗?不,你拥有了所有的信息。你可以通过分析继续计算平均值。因为你的样本是总体,这样统计量就是参数。你正在处理的纯粹是事实问题。由于拥有准确和完整的数据,因此无需进行复杂的计算。
我碰巧住在纽约市,尽可能远离树木。因此,当我面临像“精确测量所有这些树木”这样令人生畏的任务时,惰性就开始了。我真心想知道这个参数,但我反问自己:“我真的需要完全了解它还是只要测量一些树木?也许我只需对整个画面进行局部观察,以形成对该参数的最佳猜测...... 这表面上就足以完成工作要求了。”
当我这么想的时候,我在用统计学的方式思考!我永远不会知道答案。我的懒惰意味着我必须放弃获取事实或确定答案,但希望我最终会得到一些仍然有助于做决策的结果。我仍然可以把它变成一个合理的行动。这就是统计学的精髓。
无中生有?
你们当中有些人希望我会说,“有了这个神奇的公式,你就可以将不确定的变成确定!”不,当然不会。没有任何神奇的东西可以无中生有。
当我们不知道事实时,我们所能希望的是将数据与假设结合起来做出合理的决策。
假设
一个假设是描述宇宙可能的样子,但它不一定是真的。我们需要搞清楚,我们的样本是否使得之前的假设看上去很荒谬,以此判断是否要改变我们的想法,但这超出了本篇博文的范围,在这里提一下思路。

我在这里说了一些乱七八糟的话,如“所有树木的真正平均高度不到 20 米。”这是一个假设。你知道真相(我错了!)因为你在这个例子中无所不知...... 但我什么都不知道。我的陈述是一个完全有效的假设,描述了潜在的真实性。我将会在得到一些数据后才能知道自己的假设是否合理。
估计和估计量
如果知道参数,我们就不用做这些了。我们正在寻找事实,但不幸的是事实并不总能获得准确结果。由于我们无法计算参数,只能使用统计信息对其进行最佳猜测。
知道参数,我们就不用做这些了。我们正在寻找事实,但不幸的是事实并不总能获得准确结果。由于我们无法计算参数,只能使用统计信息对其进行最佳猜测。
估计是对最佳猜测的一个华丽的表述
估计只是对参数真实值的最佳猜测的一个华丽表述。这是你的猜测值,而估计量是你用于获得该数字的公式。
让我告诉你,你在统计估计方面已经非常了不起。准备好了吗?
假设你只知道其中一棵树高 23 米。你能告诉我对所有树木的真实平均高度的估计吗?
23 米?对,我也这么觉得!
如果这是我们唯一的信息,我们只能猜测 23 米;如果我们猜测其他任何数字,我们就是在胡诌。23 米是我们知道的全部,所以我们只能猜 23 米。为了得到别的东西,我们必须结合更多的信息(在这个例子中没有)或者做出假设...... 这就又是另外的事情了。
好的,我们做另一个尝试!假设我们有一个样本,我们所知道的是它的高度平均为 22.5 米。现在你最好的猜测是什么。

22.5 米?
根据几个教科书中的估计方法,包括矩法估计法,极大似然估计法等得到的最后答案和你的直觉是相同的!在现实生活中 99%以上的案例表明,只需将你的样本视为你的总体并随意使用其中的任何内容即可获得最佳猜测。你不需要任何特殊课程。棒棒哒,我们完成了!
你总是需要统计学,这是一个谎言;你不需要。如果你只是想得到最好的猜测而获得灵感,分析是你的最佳选择。摆脱 p 值,你不需要不必要的压力。
相反,你可以选择按照这些原则生活:越多(相关)数据越好,并且你的直觉非常适合做出最好的猜测,但不知道这些猜测有多准确...... 所以要保持谦虚。
但是,请不要认为我在抨击我的学科。我花了十多年的时间致力于统计学,它并不是一门一无是处的学科。
所以,在合适的时候使用统计方法才是有用的,非常有用的。
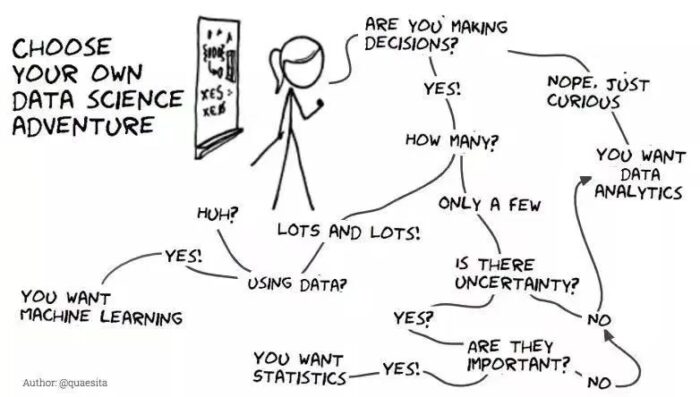
最后,你什么时候真的需要统计学呢?Cassie 也给出了这张决策图,拿好不谢👇