说到统计分析方法,卡方检验这个名字,也经常能想得起来,听得到。究其原因,一是因为常用,再有就是因为当年在学校上统计课的时候,这个方法一般是在t-检验之后就讲了,那一刻知识尚未“排山倒海”而来,就算多年在工作中用不到,在心中也还算得旧相识。根据多年的非严谨观察:记得住t-检验的同学中,颇有一部分是对卡方检验有印象的。但多数想不起t-检验为何物的同学们,差不多会把卡方检验一起忘掉。
不过卡方检验的确是有用的方法,而且,就算记得这个名字,很多同学也记不清它到底干了些什么,怎么就算出来了。为了用起来更“得其要领”,也为了科研写作行文更加严谨精彩,我们有必要把他的工作原理画出来。
卡方检验是差别性检验的统计方法,适用于分类变量的组间比较。
什么是分类变量:如果我们所观察的信息被区分为不同属性和类别的时候,记录这个信息的变量就是分类变量。比如性别,民族,分娩方式等等,都是分类变量。
就让我们从最简单的四格表开始好了。四格表就是这种有四个格子的表,两组间比较当比较的变量是二分类的时候,数据就刚好落入这四个格子。比如我们做了个社区成年人吸烟情况的抽样调查,我们想了解性别间吸烟情况是否存在不同,这个时候正是卡方检验的用武地。
首先我们需要汇总调查获得的吸烟情况(当然这不是真实的数据,我们就是为了说明这个统计方法),这实际上是一个统计描述的过程。我们通常采用例数和百分数完成数据描述,数据格式就是下边的样子:
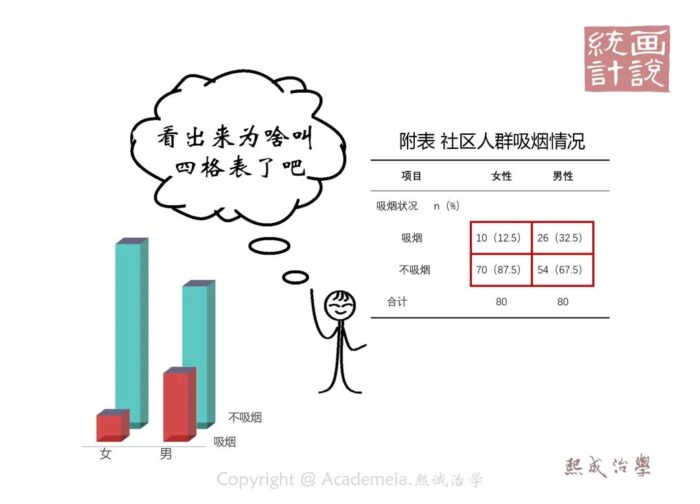
接下来就该做检验了,可为什么一定要做检验呢?男性和女性吸烟的占比不大一样,难道不是“肉眼可见”么。这就要回到假设检验的意义说起了。
在关于读懂P值的短文中我们谈到过:假设检验是我们用样本信息推断总体信息的重要方法。当我们通过样本信息试图了解总体规律的时候,抽样误差就会一直伴随着我们。所以就算对同一个总体做两次完全独立的抽样,这两个样本也几乎不可能完全一样。
所以当我们看到两个长得不大一样的样本时,自然就会问他俩本质是真的不一样还是因为抽样误差带来的呢?
假设检验就是帮我们回答这个问题的统计学手段之一。
对于以验证组间差异为目标的差别性检验,检验假设具有相同的特征和验证思路。

对于四格表卡方检验。我们期待验证的是两比较组的率或构成比(π1 ,π2)存在差异。所以永远用于放置研究预期的备择假设就是π1≠π2;同时他的对立面:π1=π2 (也就是两组没有本质不同,是来自同一总体的两个样本,所见差异由抽样误差所致)自然就是原假设。
那卡方检验又是怎么工作的呢?其实和t检验的思路挺像。咱们的原假设不是假定它俩是来自同一总体的两个样本么,那不妨把它们先看成一个样本,这个时候我们获得了一个合并后的比例关系。
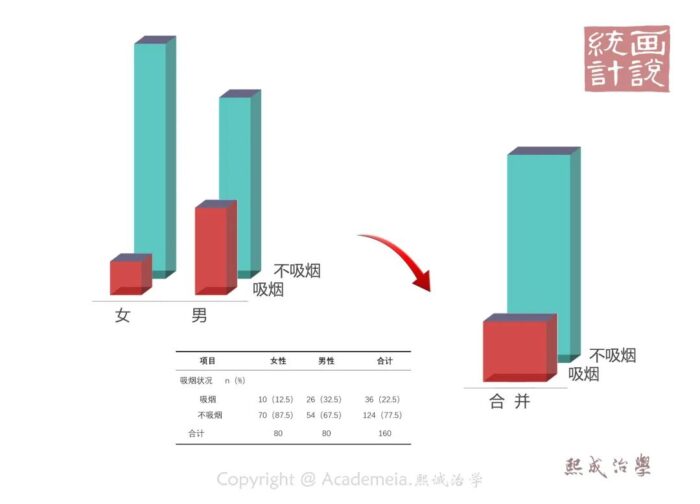
在总共160人中,一共有36人(22.5%)吸烟,124人(77.5%)不吸烟。
所以,基于原假设,两个组的构成情况是一样的,所以基于两组本质相同的原假设,两组吸烟与不吸烟的构成比例就应该都是22.5%和77.5%才对。所以从原假设的角度,两组构成完全相同,那他们“理论上”就应该是这个样子了。
然后再按照各自的样本量就能算出,他们各自“理论上”应该有的数量分布,这个参数就叫理论频数(或者亲切的叫它理论数)。既然是“理论上”的,自然可以不是整数。
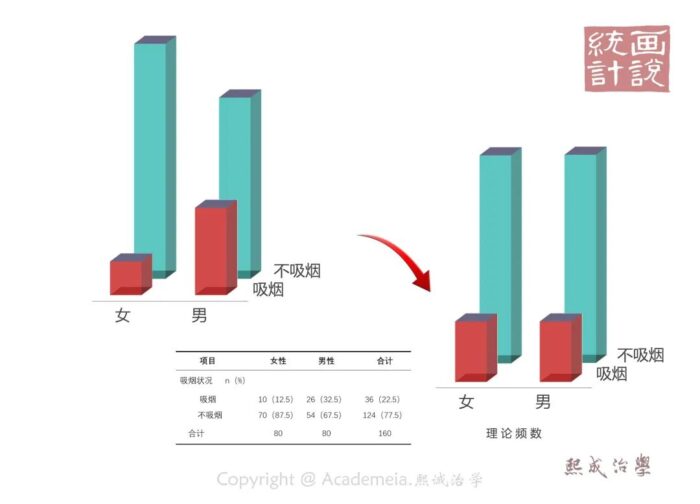
(需要说明一下:为了演示方便,样例中,男性女性两组我们设定了相同的例数,所以在相同比例下表达理论频数的柱状图,两组就完全一样。如果两组样本例数不同,这个柱子就不一样高了,但比例关系是一样的。)
通常我们从样本才得到的实际观测频数和理论频数也不会完全一样。那么这个不同是来自抽样误差的吗?
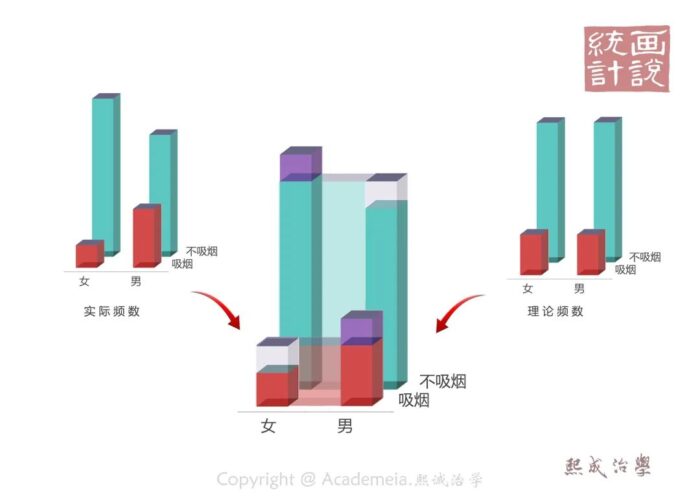
还是本质上的不同?不难理解,如果他俩本质相同,所见差异来自抽样误差,那他们更有机会彼此接近。所以,实测值相对于理论值的偏差可以帮助我们完成这个推断。
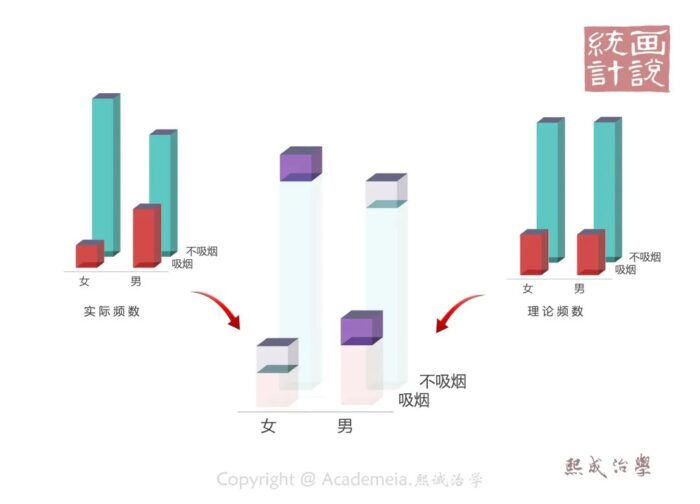
我们显然可以用实测值相对于理论值的偏差总量来表达这种差别。不过很显然这个偏差有正方向的也有负方向的。所以,通过求平方来去掉符号是我们惯用的手法。这样,统计量就构造出来了,它服从卡方分布,要不怎么叫卡方检验呢。
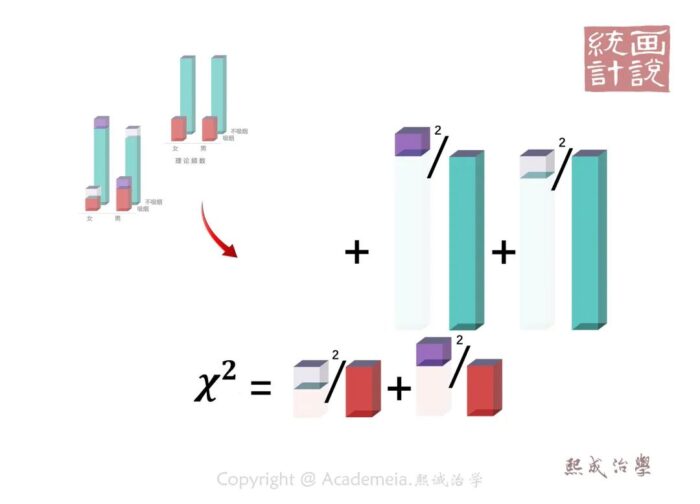
由此可见,观测频数与理论频数相去越远,卡方值越大,P值就越小。当P<0.05时,我们就拒绝原假设,接受备择假设.认为两样本是来自不同总体的抽样,差异是本质性的并非抽样误差可以解释.

还有个重要问题需要说明:卡方分布是个连续分布,所以我们在分类变量中应用卡方分布实际上是做了连续性的校正。在多数情况下,这都是可行的。
只有一种情况例外:当数据比较“稀疏”,理论频数特别低的时候。很好理解,分母特别小的时候,这个比值的变化就会异常“汹涌”,所以通常来说。纳入分析的样本总例数低于40例或者理论频数小于5的格子数超过20%的时候,通常我们会用确切概率法检验(Fisher’s Exact Test)来考察组间的不同。
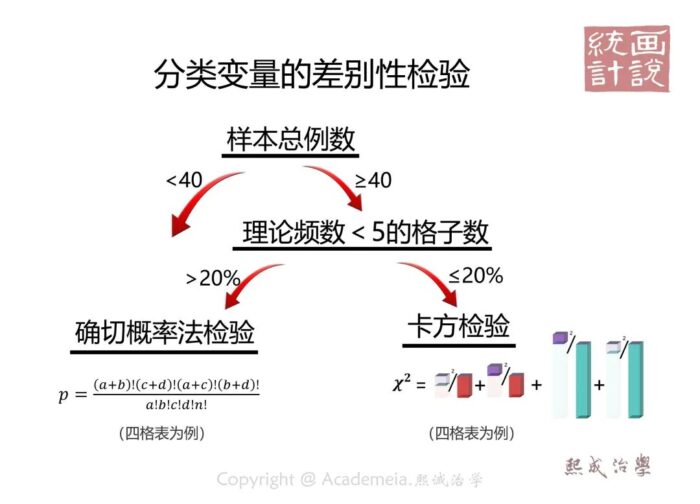
这是一个直接计算概率的分析方法,所以确切概率法结果报告时,没有象t检验,卡方检验那样的统计量。而是爽快的直指概率。它会基于现有样本所获得的行列合计为基准,把各种可能的组合列出并一一计算概率。把所有概率小于等于观测结果的概率累加起来就得到了检验结果。换言之他求得的是:基于目前观测结果,如果他俩来自同一总体,那么观测到差别如此之大以及比眼前结果差别还大的情况,一共有多少可能性。
以上,四格表检验,是我们在分析过程中最常见的一种数据格式。不过卡方检验可不是仅仅针对四格表数据的,咱们自然也可以应对多比较组多分类的情况,这时被称为行乘列表 。
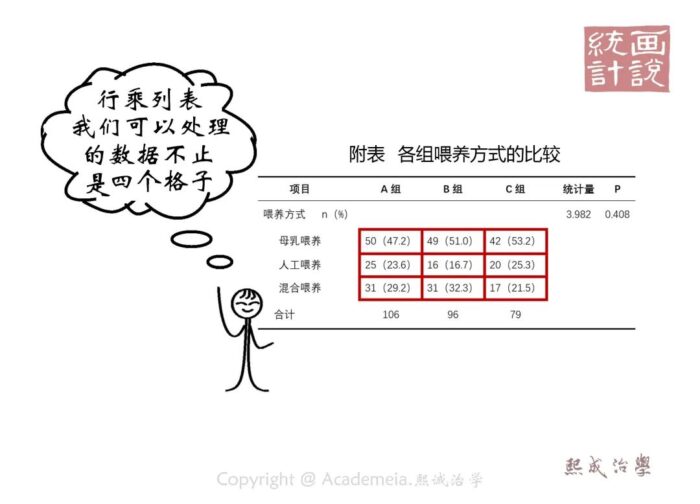
不过要特别注意的是,不要四格表用得顺手就把各种情况全都想尽办法塞进四格表,那就不大好了。
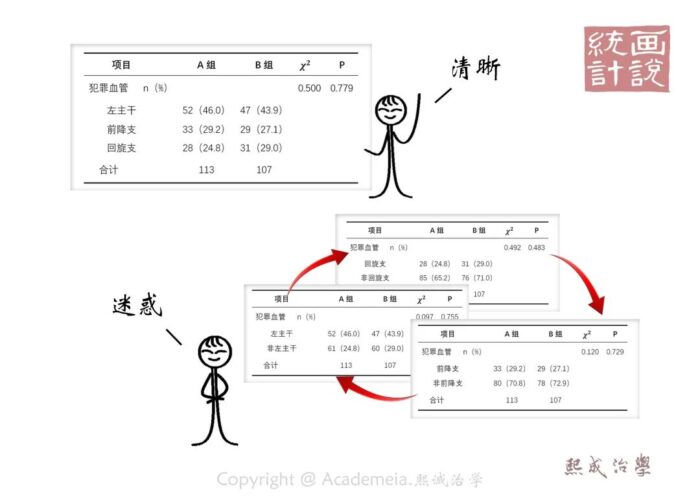
例如在比较两组病人的冠脉介入治疗病变血管分布的时候,如果根据每一个类别逐一分成是或否两类多次完成四格表检验,显然由于分类间合并原则的频繁变化,并非完备的分析逻辑。从专业意义可见,不同的犯罪血管表现了临床病变特征,他们是一个问题的不同表现形式,在比较中需要采用行乘列表的表达方式和比较方式。
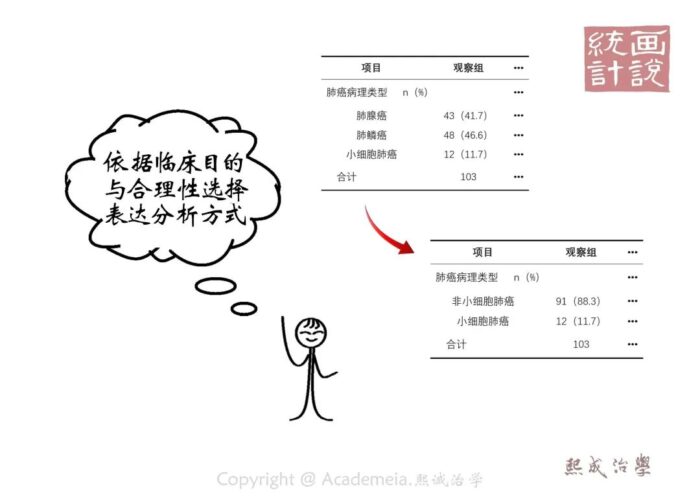
当然,在临床分析目标的指引下对多分类变量进行必要的类别间合并也是常用的方法(比如针对肺癌病理类型的分析中,有的时候会根据研究目的,依据理临床特点将病理类型合并为小细胞肺癌和非小细胞肺癌两类)。不过这一切都取决于临床意义的合理性,并需要依据分析目标的需要来决定数据的处理方法。
还有一种情况同样值得注意,卡方检验所针对的是分类变量(不同的类别间是属性不同但没有顺序关系,无程度上的不同)但我们临床上常用的数据中就还有这样一种,虽然表现上也是分了不同的类型,但他们貌似分类的外表并不妨碍他们类别间的顺序关系,比如病情的轻中重度,心功能的I.II.III.IV级。这样的等级变量,比较中一定需要考虑不同等级类别间的顺序特征,而前面提到的卡方检验则视各类别为彼此平等,比如前面的犯罪血管,性别等等,而作为等级变量出现的信息则着重于逐级递进的特点,所以比较中直接采用以上的卡方检验是不可取的。针对等级变量的组间比较需要采用趋势检验或秩和检验方可准确地反映比较的目标。


