手推公式带你轻松理解L1/L2正则化

前言

L1/L2正则化的目的是为了解决过拟合，因此我们先要明白什么是过拟合、欠拟合。

• 过拟合：训练出的模型在测试集上Loss很小，在训练集上Loss较大
• 欠拟合：训练出的模型在测试集上Loss很大，在训练集上Loss也很大
• 拟合：训练的刚刚好，在测试集上Loss很小，在训练集上Loss也很小

现在，让我们开启L1/L2正则化正则化之旅吧！

L1/L2正则化原理

L1与L2正则是通过在损失函数中增加一项对网络参数的约束，使得参数渐渐变小，模型趋于简单，以防止过拟合。

损失函数Loss：

上述Loss，MSE均方误差的Loss

L1正则化的损失函数：

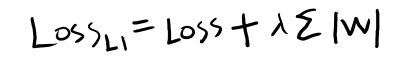
W代表网络中的参数，超参数λ需要人为指定。需要注意的是，L1使用绝对值来约束参数

L2正则化的损失函数：

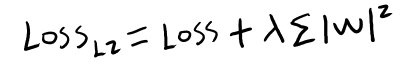
相比于L1正则化，L2正则化则使用了平方函数来约束网络参数

需要注意的是，在有的文献中，把L2正则项定义为权值向量w中各个元素的平方和然后再求平方根，其实，L2正则加不加平方根影响不大，原理都是一样的，但不加平方根更容易数学公式推导

我们知道，当W的值比较大时(即W的值距离0很远，取几百甚至几千的值)，则拟合的曲线比较陡，x稍微一变化，y的影响就比较大，如下图所示：

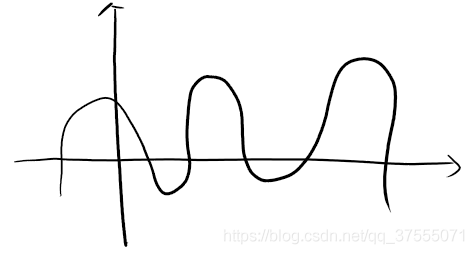
可以看到，你的模型复杂度越大，拟合的曲线就越陡，惩罚项W就越大，在这种情况容易出现过拟合，所以要避免W出现比较大的值，一个有效的方法是给loss加上一个与W本身有关的值，即L1正则项或L2正则项，这样，我们在使用梯度下降法让Loss趋近于0的时候，也必须让W越来越小，W值越小，模型拟合的曲线会越平缓，从而防止过拟合。也可以从奥卡姆剃刀原理的角度去解释，即在所有可以选择的模型中，能够很好拟合当前数据，同时又十分简单的模型才是最好的。

L1与L2正则化让W变小的原理是不同的：

• L1能产生等于0的权值，即能够剔除某些特征在模型中的作用（特征选择），即产生稀疏的效果。
• L2可以得迅速得到比较小的权值，但是难以收敛到0，所以产生的不是稀疏而是平滑的效果。

下面，从两个角度理解L1/L2正则化这两个结论

从数学的角度理解L1/L2正则化

我们来看看L1正则化的损失函数的求导及梯度更新公式：

lr是学习率(更新速率)，上述求导是Loss或Lossl1Loss_l1Lossl​1对wiw_iwi​的偏导，为了方便书写，将wiw_iwi​写成W

• 上面是加上L1正则化的损失函数后，W更新公式及loss对W求梯度的公式(准确的说是对wi求偏导)，|W|对Wi的导数是1或-1，这样W更新公式就变为加上或减去一个常量lr，
• 就是说权值每次更新都固定减少一个特定的值(比如0.01)，那么经过若干次迭代之后，权值就有可能减少到0。

L1正则化的损失函数的求导及梯度更新公式(假设$\lambda =1/4$)：

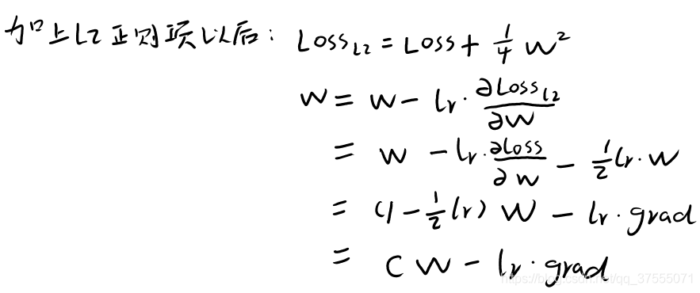
• 从上面的公式中可以看到，加上L2正则项后，W实际上每次变为原来的C倍(另一项忽略不计），假如C=0.5，那么，W每次缩小为原来的一半，虽然权值W不断变小，但是因为每次都等于上一次的一半，所以很快会收敛到较小的值但不为0。

从几何的角度理解L1/L2正则化

由于L1正则化项是∣w1 w2 ... wn∣|w_1 w_2 ... w_n|∣w1​ w2​ ... wn​∣，为了便于理解，我们假设，L1正则项是w1 w2w_1 w_2w1​ w2​，将其画在二维坐标轴上如下所示：

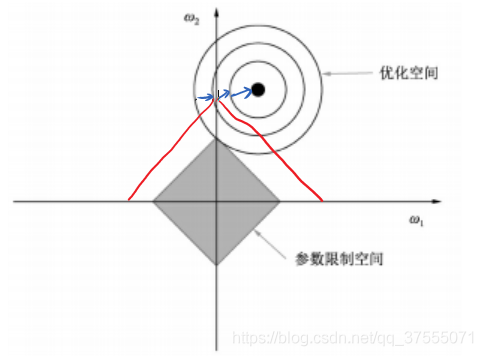
• 横轴是w1,纵轴是w2，优化空间是一个等高线图，可以看优化曲线在圆圈上移动时，只有直达W2轴的交点处，才能满足两个条件：让loss最小，让w1 w2最小，此时w2=0，所以说，L1中两个权值倾向于一个较大另一个为0即产生稀疏的效果

由于L2正则化使用了平方函数，而如果两个参数的平方和相同，呈现出的形状会是一个圆。

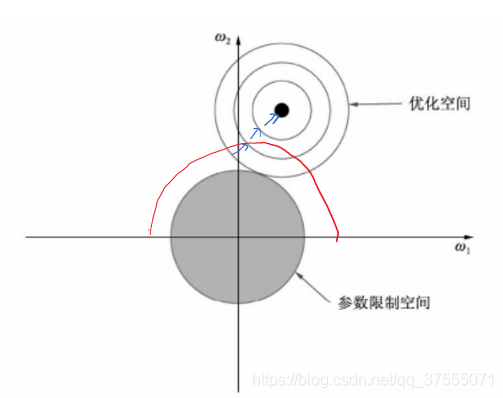
• 可以看优化曲线在圆圈上移动时，只有在两个圆圈的交点处，才能满足两个条件：让loss最小，让w1 w2w^1 w^2w1 w2最小，此时L2中两个权值都倾向于为非零的较小数，所以说，L2产生平滑的效果。

L1/L2正则化使用情形

• L1能产生等于0的权值，即能够剔除某些特征在模型中的作用（特征选择），即产生稀疏的效果，如果需要做模型的压缩，L1正则是一个不错的选择。
• 如果不做模型的压缩，在实际中更倾向于L2正则化，因为在实际操作的过程中，模型该用多少层，模型的参数量，这个不好确定，我们也不知道解决这个实际问题要用多少层网络，用多少个参数，只能去试。在试的过程中，最快最经济的做法是：在模型最开始的时候就加上正则化，不管是在欠拟合或过拟合都加上正则化，然后就不断的去训练，后面根据模型的拟合情况只要增加模型参数和模型结构就行了，不用考虑其他的，即把正则化作为默认的选项去试就可以了。