卷积神经网络(Convolutional Neueal Networks,简称CNN)可以说是神经网路模型中的"网红"网络框架，在计算机视觉方面贡献很大。卷积神经网络中的核心基础，涉及卷积层、池化层、全连接层不仅是搭建卷积神经网络的基础，也是我们需要重点掌握和理解的内容。
卷积层
举个例子,下面是一张图片以及假设对应的图片像素数值:
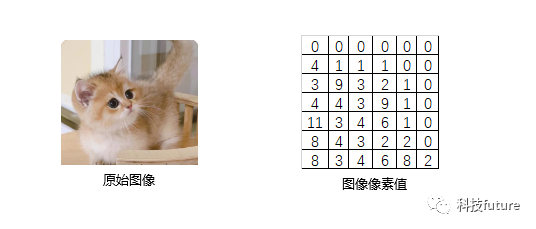
假设有有一张16x16x3的输入图像，其中32x32x3指图像的高度x宽度x通道数,通道数是RGB,也就是红色(Red)、绿色(Green)、蓝色(Blue)三个通道。下面进行图像卷积:
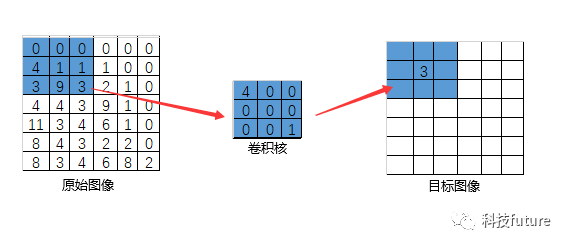注意，如果我们的原始输入数据都是图像，那么我们定义的卷积核窗口的宽度和高度要比输入图像的宽度和高度小，较为常用的卷积核窗口的宽度和高度大小是3*3和5*5。在定义卷积核的深度时，只要保证与输入图像的色彩通道保持一致就可以了。卷积核步长其实就是卷积窗口每次滑动经过的图像上的像素点数量。
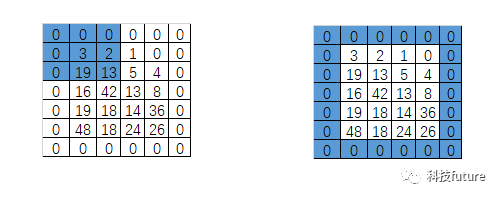可以发现上述原始图像3*3的卷积部分与卷积核进行卷积，输出的结果就是卷积窗口中的中间位置的数值，如果全部进行卷积后你会发现最终的结果会留出一圈全为0的区域，这其实是一种用于提升卷积效果的边界像素填充方式。我们在对输入图像进行卷积之前，有两种边界像素填充方式可以选择，分别是Same和Valid.
Valid方式就是直接对输入图像进行卷积，不对输入图像进行任何前期处理和像素填充，这种方式的缺点是可能会导致图像中的部分像素点不能被滑动窗口捕捉。
卷积通用公式
通过对卷积过程的计算，我们可以总结出一个通用公式，用于计算输入图像经过一轮卷积操作后的输出图像的宽度和高度的参数，公式如下:
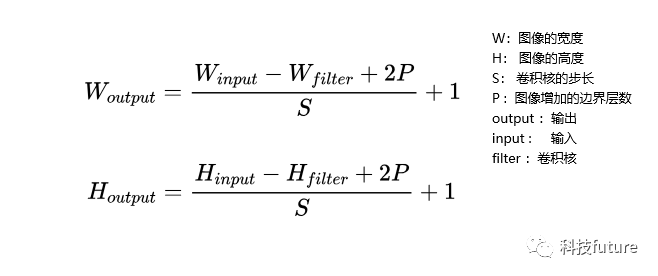
卷积层
我们已经了解了单通道的卷积操作过程，但是在实际应用中一般很少处理色彩通道只有一个的输入图像，所以接下来看看如何对三个色彩通道的输入图像进行卷积操作，三个色彩通道的输入图像的卷积过程如下:
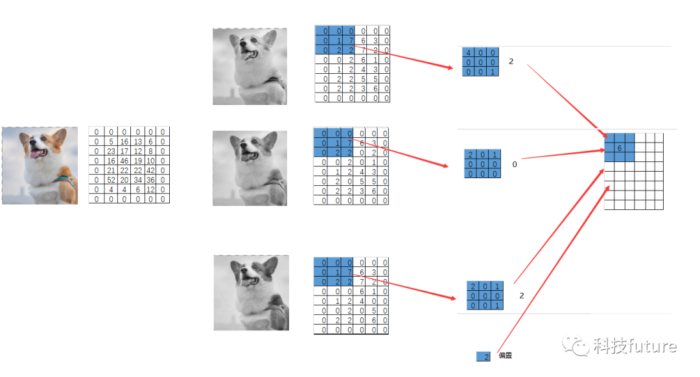在卷积过程中我们还加入一个值为2的偏置，其实整个计算过程和之前的单通道的卷积过程没多大的区别，我们可以将三通道的卷积过程看作三个独立的单通道卷积过程，最后将三个独立的通道卷积过程的结果进行相加，就得到了最后的输出结果。
池化层
池化层的输入数据一般情况下是经过卷积操作之后生成的特征图，池化层也需要定义一个类似卷积层中卷积核的滑动窗口，但是这个滑动窗口仅用来提取特征图中的重要特征，本身并没有参数。
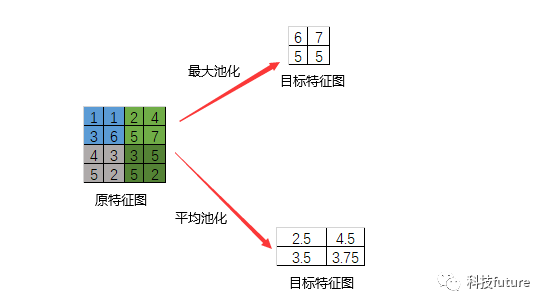首先最大池化是通过滑动窗口框选出特征图中的数据，然后将其中的最大值作为最后的输出结果。如上图所示，如果滑动窗口是步长为2的2*2窗口，则刚好可以将输入图像划分为4部分，取每部分中数字最大值作为该部分的输出结果。当然平均池化是每部分的数据相加后取平均值，并将该值作为输出结果。
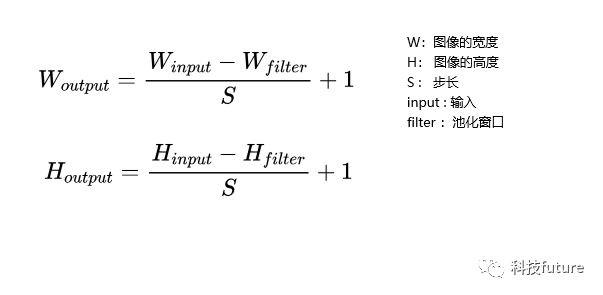
池化通用公式
全连接层
全连接层（Fully Connected Layer）是深度学习中一种基本的神经网络层，也称为密集层（Dense Layer）。全连接层的作用是将上一层的所有神经元都连接到当前层的每一个神经元上，从而实现输入与输出之间的全连接。
在全连接层中，每个输入神经元都与每个输出神经元相连接，每个连接都有一个可学习的权重和一个偏置项。这些权重和偏置项是需要通过反向传播算法进行学习的。全连接层的输出可以通过激活函数进行非线性变换，通常使用ReLU或sigmoid等激活函数。
全连接层的主要作用是将上一层的所有神经元都连接到当前层的每一个神经元上，从而实现输入与输出之间的全连接。在卷积神经网络中，全连接层通常用于将卷积层和池化层提取的特征进行压缩和分类。
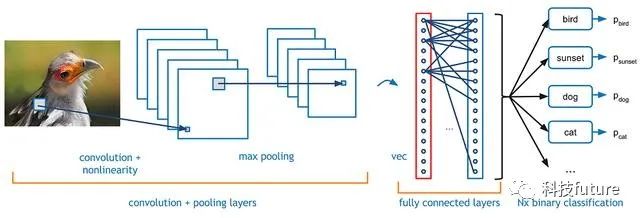
卷积神经网络整体过程
主要使用Pytorch模块进行实现,神经网络模块以及优化器、相关的图像变换，图像使用数据集来代替。
# PyTorch的主要模块 import torch # 用于构建神经网络的模块 import torch.nn as nn # 用于定义优化器的模块 import torch.optim as optim # 用于对图像进行变换的模块 import torchvision.transforms as transforms # 包含了一些常见的数据集，例如MNIST、CIFAR-10等。 import torchvision.datasets as datasets
# ===定义卷积神经网络模型
# 定义了一个名为Net的类，继承自nn.Module类
class Net(nn.Module):
def __init__(self):
# 调用父级的初始化函数
super(Net, self).__init__()
# 定义了一个卷积层，输入通道数为1，输出通道数为32，卷积核大小为3x3。
self.conv1 = nn.Conv2d(1, 32, kernel_size=3)
# 定义了一个最大池化层，池化核大小为2x2，步长为2。
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
# 定义了另一个卷积层，输入通道数为32，输出通道数为64，卷积核大小为3x3。
self.conv2 = nn.Conv2d(32, 64, kernel_size=3)
# 定义了一个全连接层，输入大小为64x5x5，输出大小为128。
self.fc1 = nn.Linear(64 * 5 * 5, 128)
# 定义了另一个全连接层，输入大小为128，输出大小为10。
self.fc2 = nn.Linear(128, 10)
# 定义了模型的前向传播函数，用于计算输入x的输出。
def forward(self, x):
# 先进行卷积操作，再进行ReLU激活操作，最后进行池化操作。
x = self.pool(nn.functional.relu(self.conv1(x)))
# 同上，再进行一次卷积操作、ReLU激活操作和池化操作。
x = self.pool(nn.functional.relu(self.conv2(x)))
# 将上一层的输出展平成一维向量。
x = x.view(-1, 64 * 5 * 5)
# 进行一次全连接操作，并进行ReLU激活操作。
x = nn.functional.relu(self.fc1(x))
# 进行另一次全连接操作，得到最终的输出。
x = self.fc2(x)
# 返回输出结果
return x数据集代替图像数据，使用MNIST数据集，也就是手写数字识别数据集用作训练集
# 加载数据集 """" 加载MNIST数据集，并进行预处理， 将输入图像的像素值进行归一化处理， 然后将数据集转换为PyTorch的DataLoader对象，以便进行批量处理。 """ # 定义了一个变换transform，先将图像转换为张量，然后对图像的像素值进行归一化处理，使得像素值的范围为[-1,1]。 transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))]) # 定义了一个训练集train_set，使用MNIST数据集， # 指定数据集存储的根目录为'./data'，train=True表示使用训练集， # download=True表示如果数据集不存在，则下载数据集，transform=transform表示对数据集进行预处理。 train_set = datasets.MNIST(root='./data', train=True, download=True, transform=transform) # 定义了一个测试集test_set，使用MNIST数据集，指定数据集存储的根目录为'./data'，train=False表示使用测试集， # download=True表示如果数据集不存在，则下载数据集，transform=transform表示对数据集进行预处理。 test_set = datasets.MNIST(root='./data', train=False, download=True, transform=transform) # 定义了一个训练集的DataLoader对象train_loader，使用train_set作为数据源，batch_size=64表示每个批次的样本数为64， # shuffle=True表示对数据进行随机打乱。 train_loader = torch.utils.data.DataLoader(train_set, batch_size=64, shuffle=True) # 定义了一个测试集的DataLoader对象test_loader，使用test_set作为数据源， # batch_size=64表示每个批次的样本数为64，shuffle=False表示不对数据进行随机打乱。 test_loader = torch.utils.data.DataLoader(test_set, batch_size=64, shuffle=False)
定义模型就是将上述的卷积神经网络模型进行实例化，使用交叉熵的方式计算损失函数，用随机梯度下降算法进行参数更新(优化器)。
# 定义了一个卷积神经网络模型model，使用之前定义的Net类进行初始化。 model = Net() # 定义了一个交叉熵损失函数criterion，用于计算模型输出与真实标签之间的损失。 criterion = nn.CrossEntropyLoss() # 定义了一个随机梯度下降优化器optimizer，使用model.parameters()获取模型参数， # lr=0.01表示学习率为0.01，momentum=0.9表示使用动量梯度下降法， # 并设置动量参数为0.9。优化器的作用是根据损失函数计算的梯度来更新模型的参数，从而使模型的输出更接近真实标签。 optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
# 进行10个epoch的训练
for epoch in range(10):
# 将running_loss置为0，用于记录每个epoch的累积损失。
running_loss = 0.0
# 遍历train_loader中的数据，使用enumerate函数获取数据的索引i和数据本身data。
for i, data in enumerate(train_loader, 0):
# 将data中的输入和标签分别赋值给inputs和labels。
inputs, labels = data
# 将优化器的梯度清零，避免梯度累加。
optimizer.zero_grad()
# 将输入数据输入到模型中进行前向传播，得到模型的输出。
outputs = model(inputs)
# 计算模型输出与真实标签之间的损失，使用之前定义的交叉熵损失函数criterion
loss = criterion(outputs, labels)
# 对损失进行反向传播，计算模型参数的梯度。
loss.backward()
# 使用优化器更新模型的参数，以减小损失
optimizer.step()
# 累加当前批次的损失到running_loss中。
running_loss = loss.item()
# 如果遍历了100个批次，则执行下面的代码。
if i % 100 == 99:
# 打印当前epoch和当前批次的平均损失。
print('[%d, %5d] loss: %.3f' % (epoch 1, i 1, running_loss / 100))
# 将running_loss置为0，用于记录下一个批次的累积损失。
running_loss = 0.0训练完成后需要测试模型是否完成训练，使用训练集作为测试集，当然你也可以使用自己的数据进行测试，防止过拟合。
# =====测试模型
# 将正确分类的样本数初始化为0。
correct = 0
# 将样本总数初始化为0。
total = 0
# 在测试过程中不需要计算梯度，因此使用torch.no_grad()上下文管理器禁用梯度计算。
with torch.no_grad():
# 遍历test_loader中的数据
for data in test_loader:
# 将data中的输入和标签分别赋值给images和labels。
images, labels = data
# 将输入数据输入到模型中进行前向传播，得到模型的输出。
outputs = model(images)
# 返回每个样本在输出中概率最大的类别，并将预测结果赋值给predicted。
_, predicted = torch.max(outputs.data, 1)
# 累加当前批次中的样本数到total中。
total = labels.size(0)
# 计算当前批次中预测正确的样本数，并累加到correct中。
correct = (predicted == labels).sum().item()
# 计算模型在测试集上的准确率，并将结果打印出来。
print('Accuracy of the network on the 10000 test images: %d %%' % (100 * correct / total))[1, 100] loss: 1.291 [1, 200] loss: 0.241 [1, 300] loss: 0.162 [1, 400] loss: 0.130 [1, 500] loss: 0.115 [1, 600] loss: 0.102 [1, 700] loss: 0.091 [1, 800] loss: 0.077 [1, 900] loss: 0.074 [2, 100] loss: 0.062 [2, 200] loss: 0.070 [2, 300] loss: 0.060 [2, 400] loss: 0.053 [2, 500] loss: 0.043 [2, 600] loss: 0.053 [2, 700] loss: 0.046 [2, 800] loss: 0.058 [2, 900] loss: 0.051 [3, 100] loss: 0.041 [3, 200] loss: 0.035 [3, 300] loss: 0.037 [3, 400] loss: 0.032 [3, 500] loss: 0.043 [3, 600] loss: 0.043 [3, 700] loss: 0.048 [3, 800] loss: 0.042 [3, 900] loss: 0.029 [4, 100] loss: 0.022 [4, 200] loss: 0.033 [4, 300] loss: 0.031 [4, 400] loss: 0.034 [4, 500] loss: 0.034 [4, 600] loss: 0.032 [4, 700] loss: 0.032 [4, 800] loss: 0.032 [4, 900] loss: 0.021 [5, 100] loss: 0.020 [5, 200] loss: 0.022 [5, 300] loss: 0.020 [5, 400] loss: 0.026 [5, 500] loss: 0.015 [5, 600] loss: 0.028 [5, 700] loss: 0.029 [5, 800] loss: 0.024 [5, 900] loss: 0.028 [6, 100] loss: 0.017 [6, 200] loss: 0.020 [6, 300] loss: 0.019 [6, 400] loss: 0.019 [6, 500] loss: 0.020 [6, 600] loss: 0.027 [6, 700] loss: 0.019 [6, 800] loss: 0.017 [6, 900] loss: 0.018 [7, 100] loss: 0.019 [7, 200] loss: 0.011 [7, 300] loss: 0.011 [7, 400] loss: 0.020 [7, 500] loss: 0.016 [7, 600] loss: 0.013 [7, 700] loss: 0.011 [7, 800] loss: 0.016 [7, 900] loss: 0.017 [8, 100] loss: 0.008 [8, 200] loss: 0.010 [8, 300] loss: 0.016 [8, 400] loss: 0.010 [8, 500] loss: 0.018 [8, 600] loss: 0.012 [8, 700] loss: 0.016 [8, 800] loss: 0.010 [8, 900] loss: 0.012 [9, 100] loss: 0.008 [9, 200] loss: 0.006 [9, 300] loss: 0.010 [9, 400] loss: 0.014 [9, 500] loss: 0.010 [9, 600] loss: 0.010 [9, 700] loss: 0.010 [9, 800] loss: 0.011 [9, 900] loss: 0.012 [10, 100] loss: 0.010 [10, 200] loss: 0.009 [10, 300] loss: 0.014 [10, 400] loss: 0.006 [10, 500] loss: 0.005 [10, 600] loss: 0.007 [10, 700] loss: 0.011 [10, 800] loss: 0.009 [10, 900] loss: 0.016 Accuracy of the network on the 10000 test images: 99 %