箱线图(Boxplot)也称箱须图(Box-whisker Plot),是利用数据中的五个统计量:最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法。它也可以粗略地看出数据是否具有有对称性,分布的离散程度等信息;特别适用于对几个样本的比较。
A boxplot is a way of summarizing a set of data measured on an interval scale. It is often used in exploratory data analysis. It is a type of graph which is used to show the shape of the distribution, its central value, and variability. The picture produced consists of the most extreme values in the data set (maximum and minimum values), the lower and upper quartiles, and the median.
可以通过箱线图的绘制过程来了解箱线图的意义:
- 绘制数轴
- 计算上四分位数(Q3),中位数,下四分位数(Q1)。
- 计算上四分位数和下四分位数之间的差值(Q3-Q1),即四分位数差(IQR,interquartile range)。
- 绘制箱线图的矩形,上限为上四分位数,下限为下四分位数。在矩形内部中位数的位置画一条横线(中位线)。
- 在Q3+1.5IQR和Q1-1.5IQR处画两条与中位线一样的线段,这两条线段为异常值截断点,称为内限;在Q3+3IQR和Q1-3IQR处画两条线段,称为外限。处于内限以外位置的点所表示的数据都是异常值(outliers),其中在内限与外限之间的异常值为温和的异常值(mild outliers),在外限以外的为极端的异常值(extreme outliers)。(注意:统计软件绘制的箱线图一般都没有标出内限和外限。)
- 在非异常值的数据中,最靠近上边缘和下边缘(即内限)的两个数值处,画横线,作为箱线图的触须。
- 从矩形的两端向外各画一条线段直到不是异常值的最远点(即上一步的触须),表示该批数据正常值的分布区间。
- 温和的异常值(即处于1.5倍-3倍四分位数差之间的异常值)用空心点表示;极端的异常值(即超出四分位数差3倍距离的异常值)用实心点(也可以用星号*)表示。
附上一张图以便利于理解:
上图中:最小值(min)=0.5;下四分位数(Q1)=7;中位数(Med)=8.5;上四分位数(Q3)=9;最大值(max)=10;平均值=8;四分位数差(interquartile range,四分位间距)=Q3 − Q1=2。
下面额外补充几个箱线图,并作简单图示:
图例1:
图例2:
图例3:
箱线图美中不足之处在于它不能提供关于数据分布偏态和尾重程度的精确度量;对于批量较大的数据集,箱线图反映的形状信息更加模糊;用中位数代表总体平均水平有一定的局限性等等。所以,应用箱线图最好结合其它描述统计工具如均值、标准差、偏度、分布函数等来描述数据集的分布形状
更多关于箱线图(boxplot)的介绍请阅读:
什么是箱线图 , 箱线图(wiki) , 箱形图(wikipedia) ,Box plot ,Box Plot ,Boxplot ,Box Plots
本文来自:http://yixf.name/2011/02/13/%E7%AE%B1%E7%BA%BF%E5%9B%BE/ (有部分删改)



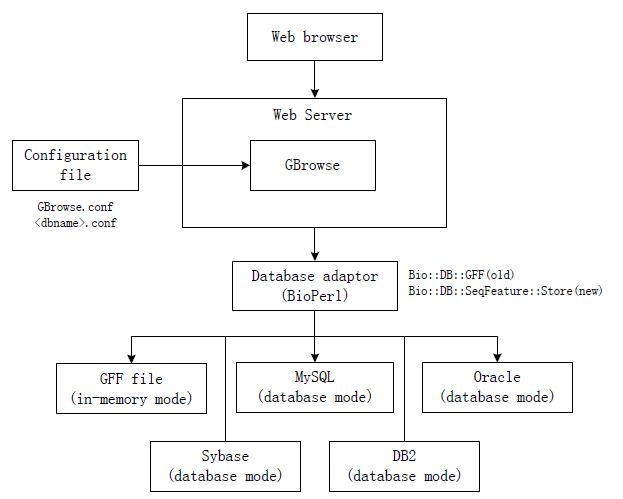
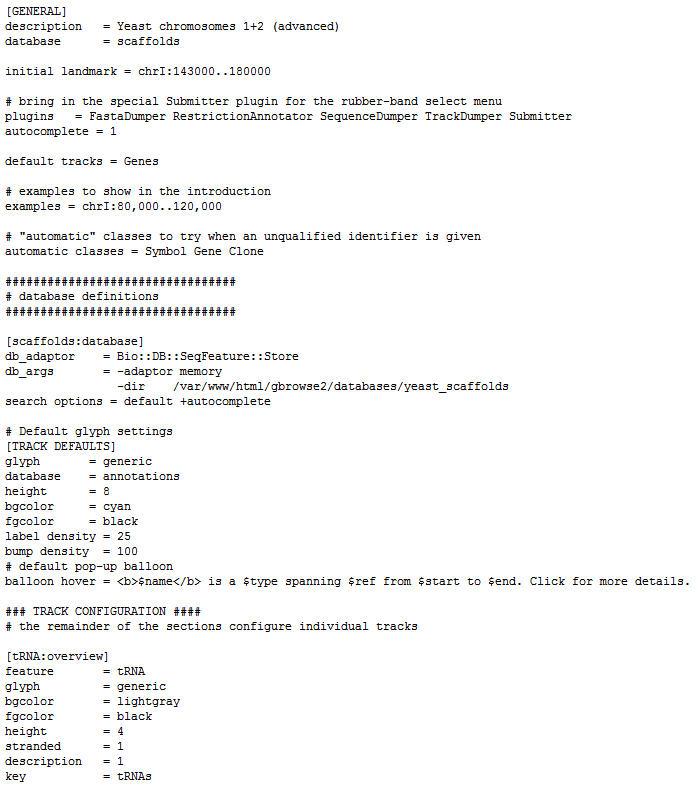
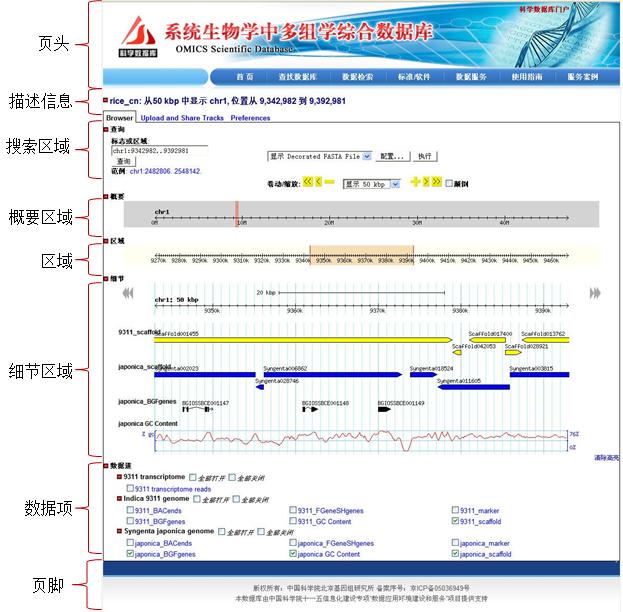

来自外部的引用