A. 主成分分析
主成分分析(principal components analysis, PCA)是一种分析、简化数据集的技术。它把原始数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是在处理观测数目小于变量数目时无法发挥作用,例如基因数据。
R语言中进行主成分分析可以采用基本的princomp函数,将结果输入到summary和plot函数中可分别得到分析结果和碎石图。但psych扩展包更具灵活性。
一、选择主成分个数
选择主成分个数通常有如下几种评判标准:
- 根据经验与理论进行选择
- 根据累积方差的门槛值,例如选择使累积方差达到80%的主成分个数。
- 根据相关系数矩阵的特征值,选择特征值大于1的主成分。
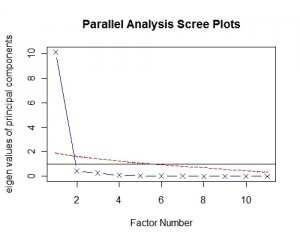
另一种较为先进的方法是平行分析(parallel analysis)。该方法首先生成若干组与原始数据结构相同的随机矩阵,求出其特征值并进行平均,然后和真实数据的特征值进行比对,根据交叉点的位置来选择主成分个数。我们选择USJudgeRatings数据集举例,首先加载psych包,然后使用fa.parallel函数绘制下图,从图中可见第一主成分位于红线上方,第二主成分位于红线下方,因此主成分数目选择1。
[code lang="R"]
fa.parallel(USJudgeRatings[,-1], fa="pc", n.iter=100, show.legend=FALSE)
[/code]
二、提取主成分
[code lang="R"]
pc=principal(USJudgeRatings[,-1],nfactors=1)
[/code]
- PC1 h2 u2
- 1 0.92 0.84 0.1565
- 2 0.91 0.83 0.1663
- 3 0.97 0.94 0.0613
- 4 0.96 0.93 0.0720
- 5 0.96 0.92 0.0763
- 6 0.98 0.97 0.0299
- 7 0.98 0.95 0.0469
- 8 1.00 0.99 0.0091
- 9 0.99 0.98 0.0196
- 10 0.89 0.80 0.2013
- 11 0.99 0.97 0.0275
从上面的结果观察到,PC1即主成分负荷,是观测变量与主成分之间的相关系数,h2是变量能被主成分解释的比例,u2则是不能解释的比例。
三、旋转主成分
旋转是将主成分负荷进行变换,以方便解释。可分为正交旋转和斜交旋转。正交旋转的流行方法是方差最大化,需要在principal中增加rotate='varimax'参数
四、计算主成分得分
主成分得分是各变量的线性组合,需在principal中增加score参数,结果将存放在scores中。但注意如果输入数据不是原始数据时,则无法计算主成分得分。
B. 探索性因子分析
探索性因子分析(Exploratory Factor Analysis,EFA)是一项用来找出多元观测变量的本质结构、并进行处理降维的技术。 因而,EFA能够将将具有错综复杂关系的变量综合为少数几个核心因子。
EFA和PCA的区别在于:PCA中的主成分是原始观测变量的线性组合,组合的选择是在各主成分无关条件下使其方差最大化。而EFA中的因子是影响原始观测变量的潜在变量,变量中不能被因子所解释的部分称为误差,因子和误差均不能直接观察到。进行EFA需要大量的样本,一般经验认为如何估计因子的数目为N,则需要有5N到10N的样本数目。
虽然EFA和PCA有本质上的区别,但在分析流程上有相似之处。下面我们用ability.cov这个心理测量数据举例,其变量是对人的六种能力,例如阅读和拼写进行了测验,其数据是一个协方差矩阵而非原始数据。R语言中stats包中的factanal函数可以完成这项工作,但这里我们使用更为灵活的psych包。
一、选择因子个数
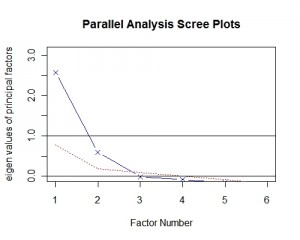
一般选择因子个数可以根据相关系数矩阵的特征值,特征值大于0则可选择做为因子。我们使用平行分析法(parallel analysis)。该方法首先生成若干组与原始数据结构相同的随机矩阵,求出其特征值并进行平均,然后和真实数据的特征值进行比对,根据交叉点的位置来选择因子个数。根据下图我们可以观察到特征值与红线的关系,有两个因子都位于红线上方,显然应该选择两个因子。
library(psych)
covariances <- ability.cov$cov
correlations <- cov2cor(covariances)
fa.parallel(correlations, n.obs=112, fa="fa", n.iter=100,show.legend=FALSE)
[/code]
其中:
library(psych)下载:http://inside-r.org/packages/cran/psych
ability.cov:http://inside-r.org/r-doc/datasets/ability.cov
cov2cor:http://inside-r.org/r-doc/stats/cov2cor
二、提取因子
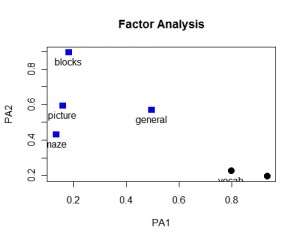
psych包中是使用fa函数来提取因子,将nfactors参数设定因子数为2,rotate参数设定了因子旋转,最后的fm表示分析方法,由于极大似然方法有时不能收敛,所以此处设为迭代主轴方法。从下面的结果中可以观察到两个因子解释了60%的总方差。Reading和vocabulary这两个变量于第一项因子有关,而picture、blocks和maze变量与第二项因子有关,general变量于两个因子都有关系。
fa = fa(correlations,nfactors=2,rotate="varimax",fm="pa" )
[/code]
- PA1 PA2 h2 u2
- general 0.49 0.57 0.57 0.432
- picture 0.16 0.59 0.38 0.623
- blocks 0.18 0.89 0.83 0.166
- maze 0.13 0.43 0.20 0.798
- reading 0.93 0.20 0.91 0.089
- vocab 0.80 0.23 0.69 0.313
- PA1 PA2
- SS loadings 1.83 1.75
- Proportion Var 0.30 0.29
- Cumulative Var 0.30 0.60
还可以用图形来表示因子和变量之间的关系
[code lang="R"]
factor.plot(fa,labels=rownames(fa$loadings))
[/code]
三、因子得分
如果输入的是原始数据,则可以在fa函数中设置score=T参数来获得因子得分。因子和原始变量之间的权重关系则存在结果的weights元素中。
C. 多维标度分析
多维标度分析(MDS)是一种将多维空间的研究对象简化到低维空间进行定位、分析和归类,同时又保留对象间原始关系的数据分析方法。
设想一下如果我们在欧氏空间中已知一些点的座标,由此可以求出欧氏距离。那么反过来,已知距离应该也能得到这些点之间的关系。这种距离可以是古典的欧氏距离,也可以是广义上的“距离”。MDS就是在尽量保持这种高维度“距离”的同时,将数据在低维度上展现出来。从这种意义上来讲,主成分分析也是多维标度分析的一个特例。
一、距离的度量
多元分析中常用有以下几种距离,即绝对值距离、欧氏距离(euclidean)、马氏距离(manhattan)、 两项距离(binary)、明氏距离(minkowski)。在R中通常使用disk函数得到样本之间的距离。MDS就是对距离矩阵进行分析,以展现并解释数据的内在结构。
在经典MDS中,距离是数值数据表示,将其看作是欧氏距离。在R中stats包的cmdscale函数实现了经典MDS。它是根据各点的欧氏距离,在低维空间中寻找各点座标,而尽量保持距离不变。
非度量MDS方法中,“距离"不再看作数值数据,而只是顺序数据。例如在心理学实验中,受试者只能回答非常同意、同意、不同意、非常不同意这几种答案。在这种情况下,经典MDS不再有效。Kruskal在1964年提出了一种算法来解决这个问题。在R中MASS包的isoMDS函数可以实现这种算法,另一种流行的算法是由sammon函数实现的。
二、经典MDS
下面我们以HSAUR2包中的watervoles数据来举例。该数据是一个相似矩阵,表示了不同地区水田鼠的相似程度。首先加载数据然后用cmdscales进行分析。
library(ggplot2)
data(watervoles, package = "HSAUR2")
data(watervoles)
voles.mds=cmdscale(watervoles,k=13,eig=T)
[/code]
下面计算前两个特征值在所有特征值中的比例,这是为了检测能否用两个维度的距离来表示高维空间中距离,如果达到了0.8左右则表示是合适的。
[code lang="R"]
sum(abs(voles.mds$eig[1:2]))/sum(abs(voles.mds$eig))
sum((voles.mds$eig[1:2])^2)/sum((voles.mds$eig)^2)
[/code]
然后从结果中提取前两个维度的座标,用ggplot包进行绘图。
[code lang="R"]
x = voles.mds$points[,1]
y = voles.mds$points[,2]
p=ggplot(data.frame(x,y),aes(x,y,label = colnames(watervoles)))
p+geom_point(shape=16,size=3,colour='red')+
geom_text(hjust=-0.1,vjust=0.5,alpha=0.5)
[/code]
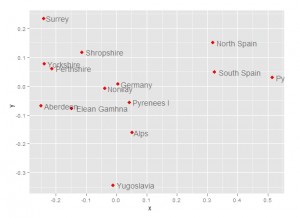
三、非度量MDS
第二例子中的数据是关于新泽西州议员投票行为的相似矩阵,这里我们用MASS包中的isoMDS函数进行分析
[code lang="R"]
library("MASS")
data(voting, package = "HSAUR2")
voting_mds = isoMDS(voting)
x = voting_mds$points[,1]
y = voting_mds$points[,2]
g=ggplot(data.frame(x,y),aes(x,y,label = colnames(voting)))
g+geom_point(shape=16,size=3,colour='red')+
geom_text(hjust=-0.1,vjust=0.5,alpha=0.5)
[/code]
D. 判别分析
判别分析(discriminant analysis)是一种分类技术。它通过一个已知类别的“训练样本”来建立判别准则,并通过预测变量来为未知类别的数据进行分类。
判别分析的方法大体上有三类,即Fisher判别、Bayes判别和距离判别。Fisher判别思想是投影降维,使多维问题简化为一维问题来处理。选择一个适当的投影轴,使所有的样品点都投影到这个轴上得到一个投影值。对这个投影轴的方向的要求是:使每一组内的投影值所形成的组内离差尽可能小,而不同组间的投影值所形成的类间离差尽可能大。Bayes判别思想是根据先验概率求出后验概率,并依据后验概率分布作出统计推断。距离判别思想是根据已知分类的数据计算各类别的重心,对未知分类的数据,计算它与各类重心的距离,与某个重心距离最近则归于该类。
1.线性判别
当不同类样本的协方差矩阵相同时,我们可以在R中使用MASS包的lda函数实现线性判别。lda函数以Bayes判别思想为基础。当分类只有两种且总体服从多元正态分布条件下,Bayes判别与Fisher判别、距离判别是等价的。本例使用iris数据集来对花的品种进行分类。首先载入MASS包,建立判别模型,其中的prior参数表示先验概率。然后利用table函数建立混淆矩阵,比对真实类别和预测类别。
library(MASS)
model1=lda(Species~.,data=iris,prior=c(1,1,1)/3)
table(Species,predict(model1)$class)
[/code]
- Species setosa versicolor virginica
- setosa 50 0 0
- versicolor 0 48 2
- virginica 0 1 49
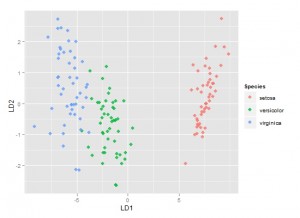
从以上结果可观察到判断错误的样本只有三个。在判别函数建立后,还可以类似主成分分析那样对判别得分进行绘图
[code lang="R"]
ld=predict(model1)$x
p=ggplot(cbind(iris,as.data.frame(ld))
,aes(x=LD1,y=LD2))
p+geom_point(aes(colour=Species),alpha=0.8,size=3)
[/code]
2.二次判别
当不同类样本的协方差矩阵不同时,则应该使用二次判别。
model2=qda(Species~.,data=iris,cv=T)
[/code]
这里将CV参数设置为T,是使用留一交叉检验(leave-one-out cross-validation),并自动生成预测值。这种条件下生成的混淆矩阵较为可靠。此外还可以使用predict(model)$posterior提取后验概率。
在使用lda和qda函数时注意:其假设是总体服从多元正态分布,若不满足的话则谨慎使用。
参考资料:
Modern Applied Statistics With S
Data_Analysis_and_Graphics_Using_R__An_Example_Based_Approach
E. 聚类分析
聚类分析(Cluster Analysis)是根据“物以类聚”的道理,对样品或指标进行分类的一种多元统计分析方法,它是在没有先验知识的情况下,对样本按各自的特性来进行合理的分类。
聚类分析被应用于很多方面,在商业上,聚类分析被用来发现不同的客户群,并且通过购买模式刻画不同的客户群的特征;在生物上,聚类分析被用来动植物分类和对基因进行分类,获取对种群固有结构的认识;在因特网应用上,聚类分析被用来在网上进行文档归类来修复信息。
聚类分析有两种主要计算方法,分别是凝聚层次聚类(Agglomerative hierarchical method)和K均值聚类(K-Means)。
一、层次聚类
层次聚类又称为系统聚类,首先要定义样本之间的距离关系,距离较近的归为一类,较远的则属于不同的类。可用于定义“距离”的统计量包括了欧氏距离(euclidean)、马氏距离(manhattan)、 两项距离(binary)、明氏距离(minkowski)。还包括相关系数和夹角余弦。
层次聚类首先将每个样本单独作为一类,然后将不同类之间距离最近的进行合并,合并后重新计算类间距离。这个过程一直持续到将所有样本归为一类为止。在计算类间距离时则有六种不同的方法,分别是最短距离法、最长距离法、类平均法、重心法、中间距离法、离差平方和法。
下面我们用iris数据集来进行聚类分析,在R语言中所用到的函数为hclust。首先提取iris数据中的4个数值变量,然后计算其欧氏距离矩阵。然后将矩阵绘制热图,从图中可以看到颜色越深表示样本间距离越近,大致上可以区分出三到四个区块,其样本之间比较接近。
data=iris[,-5]
dist.e=dist(data,method='euclidean')
heatmap(as.matrix(dist.e),labRow = F, labCol = F)
[/code]
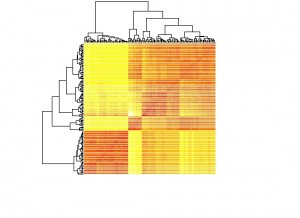
然后使用hclust函数建立聚类模型,结果存在model1变量中,其中ward参数是将类间距离计算方法设置为离差平方和法。使用plot(model1)可以绘制出聚类树图。如果我们希望将类别设为3类,可以使用cutree函数提取每个样本所属的类别。
[code lang="R"]
model1=hclust(dist.e,method='ward')
result=cutree(model1,k=3)
[/code]
为了显示聚类的效果,我们可以结合多维标度和聚类的结果。先将数据用MDS进行降维,然后以不同的的形状表示原本的分类,用不同的颜色来表示聚类的结果。可以看到setose品种聚类很成功,但有一些virginica品种的花被错误和virginica品种聚类到一起。
[code lang="R"]
mds=cmdscale(dist.e,k=2,eig=T)
x = mds$points[,1]
y = mds$points[,2]
library(ggplot2)
p=ggplot(data.frame(x,y),aes(x,y))
p+geom_point(size=3,alpha=0.8,
aes(colour=factor(result),
shape=iris$Species))
[/code]
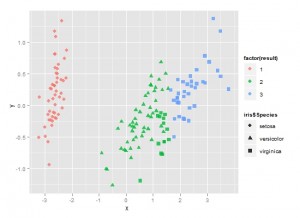
二、K均值聚类
K均值聚类又称为动态聚类,它的计算方法较为简单,也不需要输入距离矩阵。首先要指定聚类的分类个数N,随机取N个样本作为初始类的中心,计算各样本与类中心的距离并进行归类,所有样本划分完成后重新计算类中心,重复这个过程直到类中心不再变化。
在R中使用kmeans函数进行K均值聚类,centers参数用来设置分类个数,nstart参数用来设置取随机初始中心的次数,其默认值为1,但取较多的次数可以改善聚类效果。model2$cluster可以用来提取每个样本所属的类别。
[code lang="R"]
model2=kmeans(data,centers=3,nstart=10)
[/code]
使用K均值聚类时需要注意,只有在类的平均值被定义的情况下才能使用,还要求事先给出分类个数。一种方法是先用层次聚类以决定个数,再用K均值聚类加以改进。或者以轮廓系数来判断分类个数。改善聚类的方法还包括对原始数据进行变换,如对数据进行降维后再实施聚类。
cluster扩展包中也有许多函数可用于聚类分析,如agnes函数可用于凝聚层次聚类,diana可用于划分层次聚类,pam可用于K均值聚类,fanny用于模糊聚类。
来源:http://xccds1977.blogspot.com