线性回归可能是数据分析中最为常用的工具了,如果你认为手上的数据存在着线性定量关系,不妨先画个散点图观察一下,然后用线性回归加以分析。下面简单介绍一下如何在R中进行线性回归。
一、回归建模
我们利用R语言中内置的trees数据,其中包含了Volume(体积)、Girth(树围)、Height(树高)这三个变量,我们希望以体积为因变量,树围为自变量进行线性回归。
[code lang="R"]
plot(Volume~Girth,data=trees,pch=16,col='red')
model=lm(Volume~Girth,data=trees)
abline(model,lty=2)
summary(model)
[/code]
首先绘制了两变量的散点图,然后用lm函数建立线性回归模型,并将回归直线加在原图上,最后用summary将模型结果进行了展示,从变量P值和F统计量可得回归模型是显著的。但截距项不应该为负数,所以也可以用下面方法将截距强制为0。
[code lang="R"]
model2=lm(Volume~Girth-1,data=trees)
[/code]
二、模型诊断
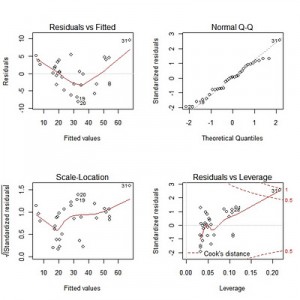
在模型建立后会利用各种方式来检验模型的正确性,对残差进行分析是常见的方法,下面我们来生成四种用于模型诊断的图形。
[code lang="R"]
par(mfrow=c(2,2))
plot(model)
par(mfrow=c(1,1))
[/code]
这里左上图是残差对拟合值作图,整体呈现出一种先下降后下升的模式,显示残差中可能还存在未提炼出来的影响因素。右上图残差QQ图,用以观察残差是否符合正态分布。左下图是标准化残差对拟合值,用于判断模型残差是否等方差。右下图是标准化残差对杠杆值,虚线表示的cooks距离等高线。我们发现31号样本有较大的影响。
三、变量变换
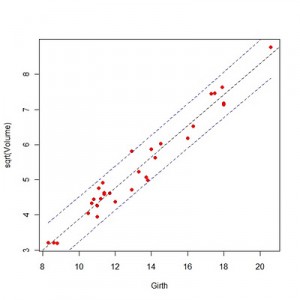
因为31号样本有着高影响力,为了降低其影响,一种方法就是将变量进行开方变换来改善回归结果,从残差标准误到残差图,各项观察都说明变换是有效的。
[code lang="R"]
plot(sqrt(Volume)~Girth,data=trees,pch=16,col='red')
model2=lm(sqrt(Volume)~Girth,data=trees)
abline(model2,lty=2)
summary(model2)
[/code]
四、模型预测
下面根据上述模型计算预测值以及置信区间,predict函数可以获得模型的预测值,加入参数可以得到预测区间
[code lang="R"]
plot(sqrt(Volume)~Girth,data=trees,pch=16,col='red')
model2=lm(sqrt(Volume)~Girth,data=trees)
data.pre=data.frame(predict(model2,interval='prediction'))
lines(data.pre$lwr~trees$Girth,col='blue',lty=2)
lines(data.pre$upr~trees$Girth,col='blue',lty=2)
[/code]
我们还可以将树围和树高都加入到模型中去,进行多元回归。如果要考虑的变量很多,可以用step函数进行变量筛选,它是以AIC作为评价指标来判断一个变量是否应该加入模型,建议使用这种自动判断函数时要谨慎。对于嵌套模型,还可以使用anova建立方差分析表来比较模型。对于变量变换的形式,则可以使用MASS扩展包中的boxcox函数来进行COX变换。
本文来自:http://www.r-bloggers.com/lang/chinese/546