1、W检验(Shapiro–Wilk (夏皮罗–威克尔 ) W统计量检验)
结果含义:当p值小于某个显著性水平α(比如0.05)时,则认为
样本不是来自正态分布的总体,否则则承认样本来自正态分布的总体。
2、K检验(经验分布的Kolmogorov-Smirnov检验)
R函数:ks.test(),如果P值很小,说明拒绝原假设,表明数据不符合F(n,m)分布。
3、相关性检验:
R函数:cor.test()
- cor.test(x, y,
- alternative = c("two.sided", "less", "greater"),
- method = c("pearson", "kendall", "spearman"),
- exact = NULL, conf.level = 0.95, ...)
结果含义:如果p值很小,则拒绝原假设,认为x,y是相关的。否则认为是不相关的。
4、T检验
用于正态总体均值假设检验,单样本,双样本都可以。
t.test()
- t.test(x, y = NULL,
- alternative = c("two.sided", "less", "greater"),
- mu = 0, paired = FALSE, var.equal = FALSE,
- conf.level = 0.95, ...)
结果意义:P值小于显著性水平时拒绝原假设,否则,接受原假设。具体的假设要看所选择的是双边假设还是单边假设(又分小于和大于)
5、正态总体方差检验
- t.test(x, y = NULL,
- alternative = c("two.sided", "less", "greater"),
- mu = 0, paired = FALSE, var.equal = FALSE,
- conf.level = 0.95, ...)
结果含义:P值小于显著性水平时拒绝原假设,否则,接受原假设。具体的假设要看所选择的是双边假设还是单边假设(又分小于和大于)
6、二项分布总体假设检验
- binom.test(x, n, p = 0.5,
- alternative = c("two.sided", "less", "greater"),
- conf.level = 0.95)
原假设:p=p0,p
7、Pearson 拟合优度χ2检验
- chisq.test(x, y = NULL, correct = TRUE,
- p = rep(1/length(x), length(x)), rescale.p = FALSE,
- simulate.p.value = FALSE, B = 2000)
p-值小于某个显著性水平,则表示拒绝原假设,否则接受原假设。
8、Fisher精确的独立检验:
- fisher.test(x, y = NULL, workspace = 200000, hybrid = FALSE,
- control = list(), or = 1, alternative = "two.sided",
- conf.int = TRUE, conf.level = 0.95)
原假设:X,Y相关。
9、McNemar检验:
- mcnemar.test(x, y = NULL, correct = TRUE)
原假设:两组数据的频数没有区别。
10、秩相关检验
cor.test(x, y,
alternative = c("two.sided", "less", "greater"),
method = "spearman", conf.level = 0.95, ...)
原假设:x,y相关.
11、Wilcoxon秩检验
- wilcox.test(x, y = NULL,
- alternative = c("two.sided", "less", "greater"),
- mu = 0, paired = FALSE, exact = NULL, correct = TRUE,
- conf.int = FALSE, conf.level = 0.95, ...)
原假设:中位数大于,小于,不等于mu.



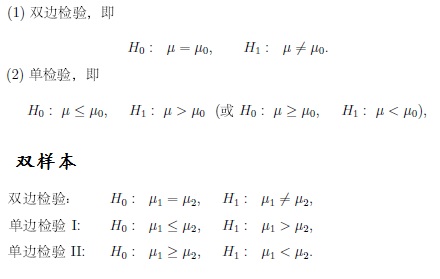
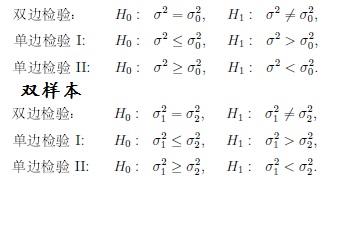
1F
怎么分享啊